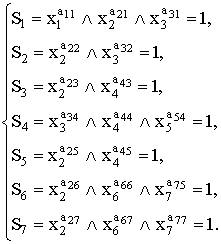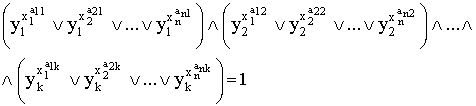Экономические науки/8. Математические методы в экономике

к.т.н. Николаенко В.Л.

Автомобильно-дорожный институт ДонНТУ, Украина

асс. Николаенко Д.В.

Автомобильно-дорожный институт ДонНТУ, Украина

ст.гр. ЭК06 Матяж Н.В.

Автомобильно-дорожный институт ДонНТУ, Украина

Использование предикатов 2-го порядка при моделировании системы учета ТМЦ

Все более глубокое проникновение в суть рассматриваемых экономических явлений неизбежно вызывающее большую сложность решаемых задач взывает к необходимости поиска новых подходов к моделированию и расширения круга математических методов, используемых при моделировании экономических явлений и сущностей.

«Экономико-математическое моделирование на это время – один из основных инструментов экономического анализа [1, 281]». Вопросами математического моделирования систем занимались такие ученые как Т. Саати [2], Ф. Морз и Д. Кимбелл [3], а так же такие как Кудрявцев Е.М. [4], Шапкин А.С., Мазаева Н.П..

В работе рассматриваются вопросы построения математических моделей состояний системы, сценариев и прецедентов в виде уравнений алгебры конечных предикатов второго порядка [5].

Ранее [6] уже решалась задача построения математических моделей состояний систем в виде уравнений алгебры конечных предикатов, дизъюнктивные нормальные формы которых были конъюнкциями предикатов узнавания состояний объектов для каждого состояния системы. Что, в свою очередь, давало возможность построить модели сценариев прецедента и, путем образования дизъюнкции конъюнктивных членов моделей сценариев, построить и модель самого прецедента. Например, при рассмотрении основного сценария прецедента «подготовка договора приобретения ТМЦ» системы учета ТМЦ математические модели состояний системы имели вид (1):

(1)

При этом, с содержательной точки зрения, состояния системы интерпретируются следующим образом:

- состояние S₁ – подача заявки на приобретение ТМЦ;

- состояние S₂ – определение объема закупки;

- состояние S₃ – подача заявки в маркетинговую службу на проведение исследований;

- состояние S₄ – исследование рынка;

- состояние S₅ – передача результатов исследования;

- состояние S₆ – подготовка договора на приобретение ТМЦ;

- состояние S₇ – постановка договора на учет в службу учета выполнения договоров.

Полученные модели (1) позволяли перейти к моделированию сценариев и прецедентов системы в виде довольно громоздких алгебро-логических уравнений.

Целью работы является получение более компактных математических моделей прецедентов системы путем использование понятий алгебры конечных предикатов высоких порядков.

При построении математических моделей сценариев и прецедентов системы вводится множество переменных , и алфавит букв , где m – количество состояний системы в сценарии с максимальным их числом, k – количество сценариев в рассматриваемом прецеденте.

Каждой переменной y_k соответствует состояние S_i взятое из одного из возможных сценариев. Таким образом , где k – число сценариев, i – номер состояния.

Принимая во внимание то утверждение, что в некоторый момент времени система может развиваться по одному из возможных сценариев, и, установив, что этот момент времени соответствует некоторому состоянию системы i, построим дизъюнктивную форму вида , используя предикаты первого порядка. Поскольку каждый показатель узнавания является некоторым состоянием системы, а модель состояния системы есть предикативная форма первого порядка, мы получаем форму, в основе которой лежат предикаты второго порядка.

Образовав конъюнкции всех состояний системы, получим математическую модель прецедента в виде уравнения алгебры конечных предикатов второго порядка (2).

(2)

Уравнения, полученные вышеописанным способом, позволяют в более компактном виде представить математические модели прецедентов системы.

Литература:

1. Кундышева Е.С. Математическое моделирование в экономике: Учебное пособие./Под науч. ред. проф. Б.А.Суслакова. – М.: Издательско-торговая кооперация «Дашков и К», 2004. – 352с.

2. Саати Т.Л. Математические методы исследования операций / Пер. с англ. А.П. Гришина. – М.: Воениздат, 1963.

3. Морз Ф.М., Кимбелл Д.Е. Методы исследования операций / Пер. с англ. А.Ф. Горохова. – М: Советское радио, 1956.

4. Кудрявцев Е.М. Исследование операций в задачах, алгоритмах и программах – М.: «Радио и связь», 1983. – 182с.

5. Шабанов-Кушнаренко Ю.П. Теория интеллекта. Проблемы и перспективы– Х.: Вища шк. Изд-во при Харьк. ун-те, 1987. – 160с.

6. Николаенко В.Л., Николаенко Д.В. Моделирование сценариев и прецедентов экономических систем. // Экономико-организационные проблемы проектирования и применения информационных систем. Ростов н/Д.:Ростовский государственный экономический университет «РИНХ», 2006. - с. 59-63