Андреев А.А., кандидат физико-математических наук

Ермаков С.В., магистр инженер-педагог

Подольский государственный аграрно-технический университет, Украина

Анализ системы специальных приемов повышения эффективности восприятия учебного материала

Проблема повышения эффективности восприятия учебного материала во время занятий являлась и является одной из наиболее актуальной. Проблема многофакторна и зависит не только от объективных условий, но и от субъективных параметров обучаемого. Безусловно, на тех или иных уровнях проблема решалась во все времена. Настоящая работа раскрывает возможности управления эффективностью восприятия ученого материала путем анализа математической модели [1] учебного процесса. В работе использована модель и обозначения, примененные в [1; 2].

Итак, объем воспринятой обучаемым информации Т (условно, за урок) можно записать[1]:

(1)

Здесь - площадь каналов восприятия вне урока; - увеличение площади при попадании ученика в мотивационное поле на уроке; β – коэффициент пропорциональности.

Экспоненциальный множитель в подынтегральном выражении отвечает за «надежность» восприятия учебного материала. Для биологической системы «обучаемый» более точным было бы применения распределения Вейбулы. Для площади каналов восприятия также выполняется закон Вебера-Фехнера

(2)

Здесь - мотивационное поле на уроке, - пороговое значение поля.

Рассмотрим «нулевую» ситуацию: преподаватель – «магнитофон», который обеспечивает постоянное мотивационное поле , ученик «диктофон» с шириной каналов восприятия, определяемой выражением (2) для этой ситуации. Понятно, что

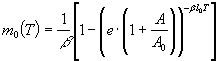(3)

Здесь е=2,718… - основа натурального логарифма.

В случае «идеальной аппаратуры» (β→0) , в случае «бесконечно длинного урока» (Т→∞) . «Детская болезнь» начинающих учителей: если очень долго учить, а ученик «все запоминает» (Т→∞, β→0), то можно даже самого слабого ученика научить практически всему (→∞). Отсюда процедуры «оставить на повторный курс», отчасти мудрость «повторение – мать учения» и т.п. – малоэффективные и энергоемкие мероприятия, которые если и дают какой-то эффект, то только при условии изменения правил игры.

Качественная зависимость приведена на рисунке 1. Ситуация β₀ соответствует планируемому объему усвоенного материала («цель занятия достигнута»). Интересным является случай β_Г, ярко описанный Ив.Франко [3]. Сколько не обучай Грицька, а его объем усвоенных «знаний» за уровень «А баба-галамага» не поднимется. И нельзя в этом винить Грицька – параметр β сформирован в нем природой.

Рисунок 1. Качественная зависимость (3). Ситуация β_Г соответствует описанной в рассказе Ив.Франко. Ситуация β₁ – плановый объем информации, полученой за урок.

Рассмотрим гипотетический случай: учитель применяет к такому ученику некий набор специальных приемов, препятствующих «забыванию», т.е. уменьшающих β. Безусловно, также спецприемы существуют и в результате их применения зависимость β(t) в линейном приближении можно записать

β(t)=β₀ – αt; α>0; αT<<β₀ (4)

α – коэффициент пропорциональности (первый член разложения β(t) в ряд Тейлора), который может определен экспериментально (в принципе). После несложных, но довольно громоздких вычислений можно записать

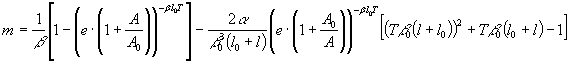(5)

Как следует из (5), второе слагаемое при начинается рост (Т) (рис.2).

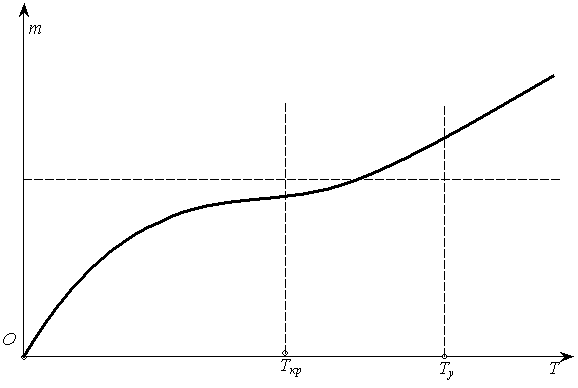
Рисунок 2. Качественная зависимость m(T) при условии проведения специальных приемов, уменьшающих «забывание»

Безусловно, мероприятия, уменьшающие процессы забывания являются довольно «тонкими» и требуют от преподавателя значительного опыта (или требуют от общества изменения мотивационных полей).

Рассмотренная выше модель является базовой для дальнейшего анализа специальных приемов для повышения эффективности процессов обучения.

Литература:

1. Андреев А.А., Ермаков С.В. Управление мотивационным полем процесса обучения. Математическая модель первого уровня // Мат. за V Межд. научн.-практ. конф. «Динамиката на современата наука – 2009», т.8 – Педагогические науки. – София, 2009. – с.70-79.

2. Андреев А.А., Ермаков С.В. Математическое моделирование процессов восприятия учебного материала // Materialy V Miedzynarodowej naukowi-practychznej konferencij “Aktualne problemy nowoczesnych nauk – 2009”? V/13/ - 2009/ Przemysl, - p.43-52

3. Ів. Франко. Вибрані твори. – Львів: Веселка, 1984