Асп. Грачев А.В., д.т.н. Руднев С.Д.

Кемеровский технологический институт пищевой промышленности

Вероятностный подход к селективному разрушению

однократным свободным ударом

Селективное разрушение растительного сырья – один из перспективных способов получения полуфабрикатов высокого качества. При создании оборудования для разрушения твердых тел актуальной является разработка математической модели, связывающей прочностные параметры компонента материала с работой внешних сил, приложенных к частицам. При свободном ударе разрушение тела наступает в результате столкновения его с рабочим органом измельчителя или другими телами в полёте. Эффект такого разрушения определяется кинетической энергией их взаимодействия и полнотой ее перехода в потенциальную энергию упругой деформации и энергию образования новой поверхности.

Рабочий орган установки представляет собой диск радиуса r с жёстко закрепленными на нём радиальными трубками. Рассмотрим процесс, в котором твёрдое тело массой m попадает в центр диска и разгоняется в трубке под действием центробежной силы. Скорость движения твёрдого тела при выходе из трубки равна:

. (1)

, (2)

где v^τ, v^r – тангенциальная и радиальная составляющие скорости тела.ω – угловая скорость вращения разгонного диска; r – радиус разгонного диска.

В результате удара об отражательные рёбра, установленные на внутренней цилиндрической поверхности корпуса, твёрдое тело разрушается или не разрушается в зависимости от установленной скорости вращения диска. Предельное напряжение σ_р при разрушении оболочки можно определить выражением:

, (3)

где F_и – сила инерции, действующая на тело в момент столкновения; S_пр – приведённая площадь поперечного сечения частицы.

Допуская, что кинетическая энергия К ударяющегося тела полностью переходит в потенциальную энергию П деформации и разрушения предположим:

(4)

Потенциальная энергия из закона Ребиндера для разрушения твёрдых тел:

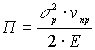, (5)

где V_пр – объём разрушаемого тела; E – модуль упругости материала.

Из равенства (3) выражаем предел прочности σ_р материала:

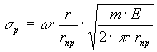, (6)

где r_пр – приведённый радиус тела.

Объектом исследований были выбраны кедровые орехи. Процесс селективного разрушения двухкомпонентных твёрдых тел с оболочкой, несвязанной с ядром, адекватно описывается графом состояний (рисунок 1), когда дробление частиц представляется как цепь случайных событий, причём условная плотность вероятности в каждый момент времени однозначно определяется своим значением только в предшествующий момент времени (свойство марковости).

Рис. 1 – Граф состояний твёрдого тела в процессе

разрушения однократным силовым воздействием

С₀ – начальное состояние твёрдого тела; С₁ – конечное состояние разрушенного однократным силовым воздействием твёрдого тела; C₂ – конечное состояние неразрушенного после удара тела; λ_ij – интенсивность перехода

из состояния C₀ в состояние C₁ и C₂

Граф состояний описывается системой дифференциальных уравнений:

,

,

.

В процессе эксперимента добивались такой скорости столкновения, когда разрушалось 50 процентов частиц материала. Отсюда условие нормировки

. , – начальные условия, , – конечные условия. Из условия нормировки .

Решая систему дифференциальных уравнений, выявляем функциональную зависимость вероятностей P_i от интенсивности λ_ij.

,

. (7)

Очевидно, что , где A – работа (энергия) рабочих органов, сообщаемая твёрдому телу.

При рассмотрении физической сущности процесса нетрудно установить, что если характеризовать отдельные состояния сыпучего материала суммарной или удельной поверхностью его тела, то λ – это скорость образования новой поверхности, имеющая размерность м²/с

, (8)

где λ_s – скорость селективного разрушения; ∆S – площадь вновь образованной поверхности; ∆t – время от начала деформирования до разрушения (время удара),

, (9)

, (10)

где δ – толщина оболочки; l – длина линий разлома; v_кр – критическая скорость движения тела, при котором происходит разрушение (определена в (2)); ∆ – линейная деформация тела в направлении удара.

В ходе решения уравнения (8) с учётом (9) и (10) получаем:

. (11)

Из равенства (4) выражаем критическую скорость движения тела, допуская что

V_пр – объём шарообразного тела,

, (12)

где R – радиус тела.

Подставляя (12) в уравнение (11), находим выражение для скорости образования новой поверхности:

.

С учётом (3), окончательно получаем

. (13)

Трудноопределяемой величиной является деформация тела в момент удара. Предлагается определить через ее через коэффициент динамичности , где σ_д – предел прочности, экспериментально определяемый по формуле (6); σ_ст – экспериментальная величина при статическом нагружении.

Отсюда , где ∆_ст – экспериментально определяемая величина критической деформации при статическом разрушении.

Подстановка (13) в (7) позволяет получить математическую модель, связывающую вероятностное определение возможности разрушения материала с геометрическими и кинематическими параметрами машины, а также прочностными свойствами материала. Принятая нормировка (P₁=P₂=0,5) позволяет определить номинальную скорость вращения рабочего органа при расчёте оборудования.

При исследовании селективного дробления кедрового ореха добивались такой энергии удара, когда скорлупа разрушалась, а ядро сохраняло целостность. Проведённые эксперименты по селективному разрушению кедрового ореха подтвердили адекватность полученной математической модели с погрешностью в допустимых пределах. Модель может быть использована для широкого спектра материалов, представляющих собой твердые тела с оболочками, несвязанными с ядром.