ЗОННАЯ МОДЕЛЬ МЕТАЛЛИЧЕСКИХ ФЕРРОМАГНИТНЫХ СТЕКОЛ

Физика/1. Теоретическая физика

А.И. Спольник, В.Г. Власенко, Л.М. Калиберда, М.А. Чегорян

Харьковский национальный технический университет

сельского хозяйства им. П. Василенко

ЗОННАЯ МОДЕЛЬ МЕТАЛЛИЧЕСКИХ ФЕРРОМАГНИТНЫХ СТЕКОЛ

Внимание к изучению ферромагнитных стекол не ослабевает. Это связано как с важностью технических приложений этих материалов, так и физическим интересом к стеклообразному состоянию вещества. Несмотря на большое число работ, посвященных монокристаллическим ферромагнетикам, многое в поведении таких веществ ещё не получило объяснения. Так не получили объяснение две аномалии, в поведении зависимости намагниченности этих объектов от температуры. Одна из таких аномалий – не соответствие между дисперсным параметром спиновой волны и коэффициентом в законе 3/2 Блоха.

Напомним прежде всего, как зависит от температуры спонтанная намагниченность ферромагнетиков с локализованными магнитными электронами (диэлектриков, 4-f металлов). В ферромагнетика с локализованными магнитными электронами (диэлектрики, 4- металлы) основной механизм уменьшения намагниченности с температурой - это возбуждение тепловых магнонов. При Т « Т_c (Т_c - температура Кюри) вклад тепловых магнонов в намагниченность М(T) содержит слагаемые, пропорциональ-ные Т^3/2, Т^5/2 . . . . . . . . , поэтому

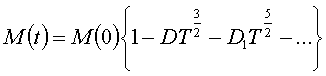. (1)

Первое слагаемое в правой части этого соотношения дает известный закон трех вторых Блоха. При этом параметр D связан с коэффициентом А в законе дисперсии спиновой волны соотношением

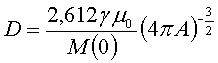(2)

(g - фактор спектроскопического расщепления).

В ферромагнетиках с коллективизированными магнитными электронами (зонных ферромагнетиках) к возбуждению тепловых магнонов добавляется еще один механизм уменьшения спонтанной намагниченности с температурой - тепловое возбуждение коллективизированных электронов. Вклад этих (называемых стонеровскими) фермиевских возбуждений приводит к уменьшению М(T) по закону [1]

где G - характеризующая ферромагнетик постоянная. Таким образом, первые члены в разложении М(T) по степеням Т имеют в таких веществах вид

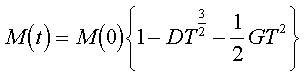. (3)

Известно [2], что в кристаллических 3d - металлах блоховский член D×T^3/2 играет роль только при очень низких температурах; в широком диапазоне температур (вплоть до Т » 0,5 Т_c) намагниченность ведет себя по характерному для зонных ферромагнетиков закону

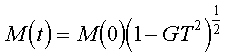Иными словами, для кристаллических 3d - металлов температурная зависимость намагниченности описывается формулой (3) (скорее, чем формулой (1)).

До сих пор анализ экспериментальных данных по намагниченности металлических стекол проводился только на основании характерного для незонных ферромагнетиков закона (1). При этом авторы большинства работ отмечают следующее противоречие: экспериментальные значения коэффициента D [3, 4] не согласуется с найденными нейтроно- графически [5] значениями параметра А. Как правило, значения D, вычисленные по формуле (2), оказываются на 30% меньше наблюдаемых. Это относится по крайней мере к богатым железом аморфным сплавам (Fe₈₀B₂₀; Fe₈₀P₁₆B₁C₃; Fe_75,4B_14,2Si_10,4); единственное известное нам исключение - богатый никелем сплав Fe₄₀Ni₄₀P₁₄B₆, в котором, согласно [6], экспериментальные значения параметров D и А не противоречат друг другу.

В свете сказанного выше о кристаллических 3d - металлах естественно попытаться интерпретировать экспериментальные данные для аморфных 3d - сплавов по формуле (3). Считая при этом коэффициент D связанным с параметром А соотношением (2), мы автоматически снимем противоречие между нейтронографическими экспериментами и измерениями намагниченности.

Входящий в (3) коэффициент G подбирается из требования, чтобы кривая (3) была максимально близка (в смысле наименьших квадратов) к эмпирической кривой М(T) = М(I-BT^3/2) (здесь и в дальнейшем М º M(0)). Если в эксперименте намагниченность наблюдалась в интервале температур (0, Т₁), то для G имеем

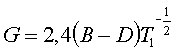. (4)

К сожалению, мы не располагаем одновременно всеми нужными экспериментальными данными (A, B, M) ни для одного аморфного ферромагнетика. В случаях, когда обе величины В и А известны из эксперимента (см.[7,8]), D = 0,7 В; поэтому величину А мы восстанавливаем

Таблица 1.

Магнитные характеристики типичных стекол.

Вещество	T_c, K	M/M₀	B/B₀	D/D₀	A/A₀	G/G₀
Fe₈₀B₂₀	685	0,74	6,47	4,53	0,45	2,23
Fe₈₀P₁₆B₁C₃	590	0,69	7,35	5,14	0,43	2,53

Таблица 2.

Параметры магнитных электронов типичных стекол

Вещество	D / D₀	g / g₀	v² / v₀²
Fe₈₀B₂₀	0,66	1,1	0,30
Fe₈₀P₁₆B₁C₃	0,63	1,1	0,27

по известному значению В в предположении, что D = 0,7 В. Эмпирические значения параметров для двух типичных ферромагнитных стекол приведены в табл. 1.

В качестве "эталонного" вещества выбрано кристаллическое ОЦК железо; соответствующие величины отмечены индексом нуль. Данные для железа: Т_С = 1042 К; М₀ = 1719 Гс; В₀ = D =3,4×10^-6 К^-3/2; А₀ = 280 мэВ×А²; G₀= 0,44 Т_C^-2.

Приведем нужные для дальнейшего соотношения теории зонного магнетизма. Для намагниченности М и коэффициента G имеем [7]

, (5)

дисперсионный параметр А равен [1]

, (6)

где D - энергия обменного расщепления спектра магнитных электронов при Т = 0, g - плотность уровней на поверхности Ферми, v - фермиевская скорость и x₁, x₂ - численные множители порядка единицы, определяющиеся законом дисперсии магнитных электронов. Соотношения (5), (6) позволяют по данным значениям А, G, М восстановить характеристики магнитных электронов:

(7)

Численные значения этих величин приведены в табл. 2. Что касается температуры Кюри, то она лишь коэффициентом порядка единицы отличается от величины D, Т_С= x₃D..

Литература

1. Stoner E.S. Collective electron ferromagnetism //Proc. Roy.Soc. (London). - 1938. - A 165, N 922. - P. 372-414.

2. Schlosser W.F. The temperature dependence of the magnetic moment of iron, Nickel and invar for T/T_C < 0,5 //Phys. Lett.- 1972. - 40 A, N 3. - P. 195-196.

3. Chien C.L., Hasegawa R. T^3/2 dependence of hyperfine field and spin-wave exitations in ferromagnetic metallic glasses //Phys. Rev.- 1977. - B16, N 5. - P. 2115-2123.

4. Hang Nam O.K., Kyung Seon Back, Chul Sung Kim. Magnetic properties and the chrystallization of amorphous Fe_75,4B_14,2Si_10,4 //Phys. Rev. - 1981. - B24, N11. - P. 6600 - 6609.

5. Webb D.J., Bhagat S.M. Spin glass behavior and nonergadicity in amorphous iron - boron allоys //Solid state commun. - 1982.- 43, N 4. - P. 239-242.

6. Kaul S.M. Detailed magnetization stydy of an amorphous ferromagnet //Phys. Rev. - 1981. - B24, N 11. - P. 6550-6565.

7. Петраковский Г.А. Аморфные магнетики //УФН.- 1981. - 134, вып. 2.-С.305-325.

8. Neutron scattering study of spin waves in the amorphous metallic ferromagnet (Fe₉₃Mo₇)₈₀B₁₀P₁₀ /J.D.Axe, Cr.Shirane, T.Mizoguchi, K.Yamauchi //Phys. Rev.- 1977.- B15, N 5. - P. 2763-2770.