Современные информационные технологии/ 2. Вычислительная техника и программирование

Л.И. Андреева, к.т.н. П.В. Желтов,

д.м.н. Г.В. Кокуркин, к.т.н. В.И. Семенов

Чувашский государственный университет, Россия.

Вейвлет-анализ сигнала частоты сердечных сокращений

В настоящее время использование в медицинской практике компьютера в сочетании с измерительной и управляющей техникой позволило создать новые эффективные средства для обеспечения автоматизированного сбора информации о состоянии пациента, ее обработки в реальном масштабе времени и управления его состоянием.

Методы вейвлет-преобразования (ВП), несмотря на сложность, связанную с математической реализуемостью и интерпретацией результата, доказали свою практическую эффективность в медицине.

Вейвлет-спектр W(a,b) одномерного сигнала S(t) представляет собой поверхность в трехмерном пространстве. Трехмерное изображение спектра позволяет анализировать свойства сигнала одновременно в физическом и частотном пространствах. При применении вейвлетов для анализа сигналов непрерывное ВП более удобно, его некоторая избыточность, связанная с непрерывным изменением масштабного коэффициента а и параметра сдвига b, становится здесь положительным качеством, так как позволяет более полно и четко представить и проанализировать сигнал[1,2].

Для исследования сигнала частоты сердечных сокращений (ЧСС), авторами используется алгоритм непрерывного быстрого вейвлет-преобразования [3,4]. Оцифрованные данные сигнала ЧСС, используются для преобразования в вейвлет-спектр W(a,b). Программы написаны на языках Visual C++ и Visual Basic for Applications для работы с электронной таблицей Excel. Операционная система – Windows XP.

Применяя МНАТ-вейвлет вычисляются коэффициенты W(a,b) сигнала ЧСС, где b меняется от 1 до 1024. Полученные вейвлет-коэффициенты (функции) W(a,b) разбиваются на сегменты фиксированной длительности (l = 8), количество сегментов n равно 128. В каждом сегменте вычисляются коэффициенты Фурье a(i), b(i) функций W(a,b), используя быстрое преобразование Фурье. Используется простейшая весовая функция (окно) Дирихле. Влияние на спектр других весовых функций (Хемминга, Бартлетта, Ханна и других) не рассматривалось.

По формуле

(1)

вычисляется Фурье-спектр функций W(a,b) каждого сегмента. Используя Фурье-спектр сигнала вычисляется энергия сегментов функций W(a,b). Энергия сегментов вычисляются по формуле

. (2)

Вычисление энергии сегментов по формуле (2) практически совпадает с нахождением дисперсии вейвлет-коэффициентов по стандартной формуле

,

где – среднее значение вейвлет-коэффициентов в сегменте.

Использование энергии сегментов при суммировании всех частот эквивалентно использованию дисперсии вейвлет-коэффициентов, так как среднее значение вейвлет-коэффициентов в сегменте близко к нулю. Положительные и отрицательные значения вейвлет-коэффициентов почти одинаковы, и поэтому среднее значение вейвлет-коэффициентов в сегменте близко к нулю. Но используя формулу (2), энергию можно вычислять для разных диапазонов частот и получать больше информации.

Результаты анализа показывают, что энергия сегментов в вейвлет-спектрах W(a,b) для людей с патологией имеют более низкое значение для больших масштабных коэффициентов. На рис. 1 представлена энергия сегментов вейвлет-спектра ЧСС для человека с патологией.

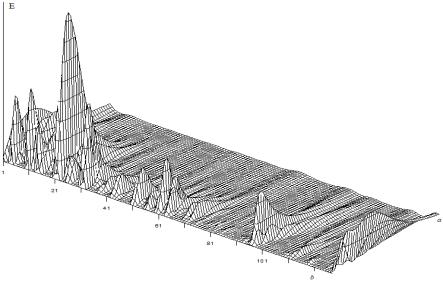
Рис. 1. Зависимость энергии сегментов W(а,b) от масштабного коэффициента а человека с патологией.

Здесь оси абсцисс соответствуют номера сегментов n, а масштабный коэффициент а меняется от 1 до 50. На рис. 1 видно, что при больших значениях а (35-50) энергия сегментов W(a,b) имеет более низкое значение по сравнению с энергиями сегментов для малых и средних значений а (1-34). На рис. 2 представлен график зависимости энергии сегментов вейвлет-спектра ЧСС для человека без патологией. На рис. 2 масштабный коэффициент а меняется от 1 до 50 с шагом 1.

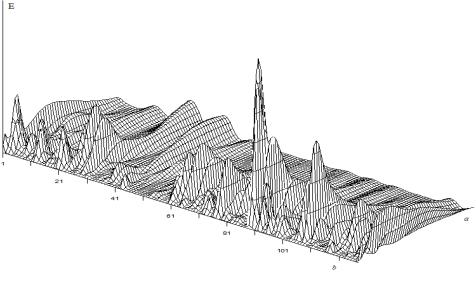
Рис. 2. Зависимость энергии сегментов W(а,b) от масштабного коэффициента а человека без патологии.

На рис. 2 видно, что энергия сегментов вейвлет-спектра ЧСС для больших масштабных коэффициентов а (30-50) не намного отличается от энергии сегментов для малых и средних значений а (1-34). Такая же картина наблюдается для других здоровых пациентов. Если есть сомнение в том, что картина соответствует больному или здоровому человеку есть возможность идентификации, используя вейвлет-спектр ЧСС для других масштабных коэффициентов а. На рис. 3 представлен график зависимости энергии сегментов вейвлет-спектра ЧСС для человека с патологией.

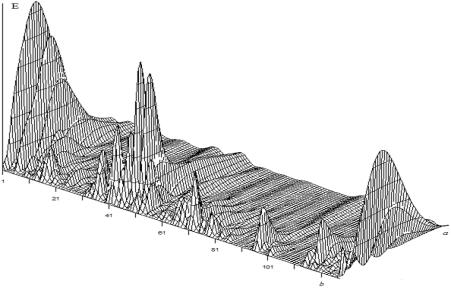
Рис. 3. Зависимость энергии сегментов W(а,b) от масштабного коэффициента а человека с патологией.

На рис. 3 масштабный коэффициент а меняется от 1 до 50 с шагом 1. На рис. 3 для больших масштабных коэффициентов а (30-50) есть сегменты в которых энергия вейвлет-коэффициентов достаточно большие. Для того, что бы проверить более точно используем зависимость энергии вейвлет-коэффициентов с большим диапазоном значений а. На рис. 4 представлен график зависимости энергии сегментов вейвлет-спектра ЧСС для того же человека, где масштабный коэффициент а меняется от 35 до 235 с шагом 4.

Рис. 4. Зависимость энергии сегментов W(а,b) от масштабного коэффициента а человека с патологией.

На рис. 4 видно, что при увеличении масштабного коэффициента а, так же как на рис. 1, энергия сегментов вейвлет-спектра ЧСС имеет низкие значения. Приведенные примеры показывают, что многомасштабное представление позволяет визуализировать динамику изменения энергии сегментов вейвлет-спектра ЧСС вдоль «оси масштабов». Эти изменения по «масштабной переменной» дают большую информацию, чем сигнал ЧСС

Литература:

1. Астафьева Н.М. Вейвлет-анализ: Основы теории и принципы применения. // УФН, т. 166, № 11, ноябрь, С. 1145 – 1170.

2. Новиков И.Я. Теория всплесков / И.Я. Новиков, В.Ю. Протасов, М.А. Скопина. М.: Физматлит, 2005. 616 с.

3. Желтов П.В. Семенов В.И. Выделение границы между гласными и согласными фонемами при распознавании речи. // Сборник научных трудов. Выпуск 1 Казань: Изд-во Казан. гос. техн. ун-та, 2008, 80с.

4. Семенов В.И. Свидетельство об официальной регистрации программ для ЭВМ № 2007615024 «Непрерывное быстрое вейвлет-преобразование».