Современные информационные технологии / Вычислительная техника и программирование

Kryuchin O.V., Vyazovova E.V., Rakitin A.A.

Tambov State University named after G.R. Derzhavin

DEVELOPMENT OF PARALLEL GRADIENT AND QUASINEWTON ALGORITHMS FOR THE ECONOMIC PROBLEM SOLVING

In this paper it suggests parallel methods training artificial neural networks based on the target function decomposition to a Teylor row. It suggests parallel algorithms for few methods which are steepest descent, QuickProp, RPROP, BFGS and DFP.

Keywords: parallel algorithms, artificial neural networks

Introduction

As we know artificial neural networks (ANNs) implement the human brain mathematical model. The human brain can solving different economic tasks for example to develop models or to forecast row (currency pair) and etc. But the modern computers mighty is not so high as the human brain mighty that is why the ANNs training needs large time expenses very often. Sometime it is not problem but in other situations it is not available. This problem solution is the clustering. The ANN which is trained on computer cluster needs less time expenses than network which is trained on personal computer. But for the training with the computer cluster usage we have develop special algorithms considering the parallel computing specific.

As far as the ANNs training is priory defined by the target function minimization, we can use gradient algorithms which are very effective in the optimization theory. These methods use the decomposition of target function to the Tailor row in the current minimum area. In the papers [1, 2] this decomposition is described by equation

	(1)

where 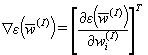is the gradient, 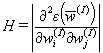is the Hessian which is the simmetric matrix consisting of second factor derivatives and is the vector defining the direction and the depending of vector values. In the real usually it calculates three first members only and ignores other.

This paper aim is to develop parallel algorithms of several methods which are the method of the steepest descent, QuickProp, RPROP, BFGS and DFP.

Gradient methods

The gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient (or of the approximate gradient) of the function at the current point. If instead one takes steps proportional to the positive of the gradient, one approaches a local maximum of that function, the procedure is then known as gradient ascent.

Gradient descent is also known as steepest descent, or the method of steepest descent. When known as the latter, gradient descent should not be confused with the method of steepest descent for approximating integrals.

Gradient descent is based on the observation that if the multivariable function is defined and differentiable in a neighborhood of a point , then decreases fastest if one goes from in the direction of the negative gradient of function at , which is . It follows that, if we have formula

	(2)

(for a small enough number) then [3, 4].

In the QuickProp algorithm changing the -th weight coefficient on the -th iteration uses formula

,	(3)

where is the coefficient minimizing weight coefficient values, is the moment factor coefficient. There are two difference from steepest descent methods. These are adders weights minimizer and moment factor [5]. Usually minimizer has value equaling to and wanted for weakening weight links, and it is necessary to have a moment factor for the algorithm adaptation to the current training results. Coefficient is unequal for each weight and its calculation consists of two steps. The first step calculates by formula

,	(4)

and the second step find the minimal value of and values. In paper [6] Falman suggests to use 1.75 as the value of .

The method RPROP idea is to ignore the gradient value and to use its sign only. In paper [4, 5] the changing of weights is calculated by formulas

	(5)
	(6)
	(7)

In the paper of Osowsky [5] it suggest values , , , .

Quisinewton methods

In optimization, quasi-Newton methods (a special case of variable metric methods) are algorithms for finding local maxima and minima of functions. Quasi-Newton methods are based on Newton's method to find the stationary point of a function, where the gradient is 0. Newton's method assumes that the function can be locally approximated as a quadratic in the region around the optimum, and uses the first and second derivatives to find the stationary point. In higher dimensions, Newton's method uses the gradient and the Hessian matrix of second derivatives of the function to be minimized.

In quasi-Newton methods the Hessian matrix does not need to be computed. The Hessian is updated by analyzing successive gradient vectors instead. Quasi-Newton methods are a generalization of the secant method to find the root of the first derivative for multidimensional problems. In multi-dimensions the secant equation is under-determined, and quasi-Newton methods differ in how they constrain the solution, typically by adding a simple low-rank update to the current estimate of the Hessianks [7].

Quasinewton algorithms calculate new weights by formula

	(8)

which is the base of the Newton optimization algorithm and is the theoretical equation because needs the positive Hessian definition in the each step. But it is not real thus we use the Hessian approximation instead it. In the each step the Hessian approximation is modified.

We will define the matrix which is reversed to the Hessian as and the gradient changing as . As it is written in papers [9, 10] in such situation new weights can be calculated by formula

	(9)

The initial matrix value is equal to one () and next values usually are calculated using formula Broyden-Fletcher-Goldfarb-Shanno

	(10)
	(11)
	(12)

We will symbolized the multiplying of changing gradient to transported changing gradient as

	(13)

the multiplying of changing weight coefficients vector to transposed changing weight coefficients vector as

	(14)

the multiplying of transposed changing weights coefficients vector to changing gradient as

	(15)

the multiplying of transposed changing gradient to matrix as

,	(16)

and the multiplying of transposed vector to gradient changing vector as

	(17)

Thus we can write equation (9) as

	(18)

In other acquainted algorithm Davidon-Fletcher-Powell [8] the matrix new value is calculated by formula

	(19)

If we will use definitions (12)-(16) then we can get equation

	(20)

Parallel algorithms

Gradient methods are based on a gradient vector calculation and change the values of the weight coefficients in the opposite direction:

	(21)

Here is the gradient.

In these algorithms the vector of weight coefficients is divided into n parts and each part is located on a different processor. The lead processor calculates weight coefficients, and the other processors calculate weights. The values of and are calculated by formulas

	(22)

and

	(23)

This idea is fully described in papers [11, 12].

Parallel quasinewton algorithms

Parallel quasinewton algorithms can be developed by two ways. The first way is to calculate values of as the typical parallel gradient algorithm (and too), to pass calculated values from non-zero to the lead processor, to calculate a value and weights changing on the lead processor and to send calculated weights to all processors. After it all processors calculate new weight values themself.

Second parallel variants of BFGS and DFP algorithms are different. The BFGS algorithm consists of fourteen steps:

1. gradient is calculated by all processors like in other gradient methods (gradient changing is calculated by all processors too);

2. all non-zero processors send calculated gradient parts to the lead processor;

3. the lead processor forms general gradient and sends its new values to all processors;

4. each processor except zero calculates its matrix rows and vector elements and then sends it to the lead; at that time the lead processor calculates new value;

5. non-lead processors pass calculated matrix rows and vector elements to the lead processor;

6. zero processor calculates new value of vector ;

7. all processors except zero calculates its matrix rows; the lead processor at that time calculates matrix

;	(24)

8. non-zero processors pass calculated elements of matrix

	(25)

to the lead processor

9. the lead processor sends matrix , scalar and vector to all other processors;

10. the lead processor calculates matrix

,	(26)

and all other processors calculate their rows of matrix

,	(27)
	(28)

and

;	(29)

11. non-lead processors pass calculated matrix rows to the lead processor;

12. the lead processor calculates matrix and weights changing ;

13. zero processor sends matrix and weights changing to all other processors;

14. all processors calculate new values of weights .

First steps of parallel DPF algorithm are equaling to BFGS algorithm steps but last steps are different:

1.

2.

3.

4.

5.

6.

7. non-zero processors calculate its matrix rows;

8. non-zero processors pass calculated rows of matrix to zero processor;

9. the lead processor forms general matrix and sends it, matrix and scalar to all processors;

10. non-lead processors calculate its rows of matrix

,	(30)
	(31)

and

	(32)

and zero processor at that time calculates

	(33)

11. matrix rows are passed from non-zero processors to the lead;

12. the lead processor calculates matrix

	(34)

and weights changing ;

13. the lead processor sends matrix and weights changing to all other processors;

14. all processors calculate new values of weights .

Conclusion

So we have developed parallel variants of few gradient and qusinewton algorithms which can be used for the artificial neural networks training.

Reference

1. Gill P., Murray W., Wrights M. Practical Optimisation. - N.Y.: Academic Press, 1981.

2. Widrow B., Stearns S. Adaptive signal processing. - N.Y.: Prentice Hall, 1985.

3. Mordecai Avriel. Nonlinear Programming: Analysis and Methods // Dover Publishing, 2003.

4. Jan A. Snyman. Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms // Springer Publishing, 2005.

5. Осовский С. Нейронные сети для обработки информации; пер. с пол. И.Д. Рудинского. - М.: Финансы и статистика, 2002. - 344 с.: ил. (Osovsky S. Neural networks for information analysis // Moscow: Finance and statistic, 2002 – 344 p.)

6. Riedmiller M., Brawn H. RPROP - a fast adaptive learning algorithms. Technacal Report // Karlsruhe: University Karlsruhe. 1992.

7. Zadeh L.A. The concept of linguistic variable and its application to approximate reasoning. Part 1-3 // Information Sciences. 1975. - Pp. 199-249.

8. Riedmiller M. Untersuchungen zu konvergenz und generalisierungsverhalten uberwachter lernverfahren mit dem SNNS. In Proceedings of the SNNS. 1993.

9. Bonnans J.F., Gilbert J.Ch., Lemarechal C., Sagastizbal C.A., Numerical optimization, theoretical and numerical aspects. // Springer: Second edition., 2006. - 437 p.

10. Davidon W.C. Variable Metric Method for Minimization // SIOPT, 1991 - Vol. 1, Iss. 1 - Pp. 1-17.

11. Крючин О.В. Разработка параллельных градиентных алгоритмов обучения искусственной нейронной сети // Электронный журнал "Исследовано в России", 096, стр. 1208-1221, 2009 г. // Режим доступа: http://zhurnal.ape.relarn.ru/articles/2009/096.pdf , свободный. – Загл. с экрана. (Kryuchin O.V. Development of parallel gradient algorithms of artificial neural network teaching // Electronic journal “Analysed in Russia”, 2009 - Pp 1208-1221 // http://zhurnal.ape.relarn.ru/articles/2009/096.pdf)

12. Крючин О.В. Параллельные алгоритмы обучения искусственных нейронных сетей с использованием градиентных методов. // Актуальные вопросы современной науки, техники и технологий. Материалы II Всероссийской научно-практической (заочной) конференции. — М.: Издательско-полиграфический комплекс НИИРРР, 2010 — 160 с., с. 81-86. (Kryuchin O.V. Parallel algorithms of artificial neural networks training with gradient methods usage // Actual problems of the modern science, technique and technology. Processings of the II AllRussian scientific-practical conference. - Moscow:NIIRRR, 2010 – 160 p, Pp 81-86)