Николаев А.В.

Ярославский государственный университет, Россия

Ограничения на целевые функции для эффективного решения задачи целочисленного программирования на многограннике, ассоциированном с задачей 3-выполнимость

Одно из направлений исследования задач комбинаторной оптимизации состоит в изучении ассоциированных с задачами выпуклых многогранников (см., например [1,2]). В работе [3] был введен релаксационный многогранник , связанный с известной NP-полной задачей 3-выполнимость. Описывающие его внешние ограничения имеют вид:

(1)

(2) (3)

(4)

где k=1,2,3; l=1,2; i,s=1,2…m; j,t=1,2…n.

Многогранник является релаксацией задачи 3-выполнимость в том смысле, что задача 3-выполнимость полиномиально сводится к задаче целочисленного программирования на .

1. Нетрудно заметить, что подробно изученный корневой полуметрический многогранник [1,2,3] изоморфен грани . Известно [1,2], что координаты нецелых вершин корневого полуметрического многогранника принимают значения только из множества . В работе [4], показывалось, что свойство ограниченности значений координат вершин не сохраняется для многогранника . А именно, была доказана теорема об экспоненциальном росте максимального знаменателя координат вершин с увеличением размерности пространства. Следствием теоремы является принципиальная трудность составления полного описания множества нецелочисленных вершин многогранника , в то время как для корневого полуметрического многогранника и для целых вершин эта задача была успешно решена [1,4]. Ниже приводится один из возможных вариантов формулировки необходимого условия для нецелочисленных вершин .

Теорема. Если точка является нецелочисленной вершиной , то найдутся такие i,j,k,l, для которых:

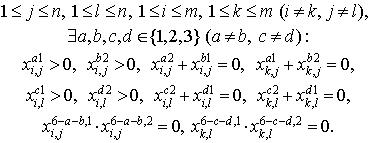
Доказательство. Напомним важный факт из теории выпуклого анализа. Крайняя точка выпуклого множества A принадлежит A, но не является внутренней ни для одного отрезка из A.

Пусть u – нецелочисленная вершина . Построим точку по вершине u, прибавив к первому столбцу каждой ячейки i-той строки , а ко второму, соответственно, . Рассмотрим строку i подробно.

1. Все ячейки i-той строки имеют нулевой столбец. Если подобный вид имеют все строки ячеек, то, очевидным образом, u – не является нецелочисленной вершиной. Без ограничения общности будем полагать, что i-тая строка не удовлетворяет этому условию.

2. Все ячейки i-той строки имеют две ненулевые координаты в одной строке. Операция выполняется элементарным образом, без изменения сумм по строкам.

3. Найдется такой столбец ячеек j, для которого: : Увеличиваем на , , уменьшаем на . При этом сумма координат по строке a увеличивается, по строке b уменьшается.

В варианте 3 мы изменили столбец j. Рассмотрим возможные варианты.

3.1. Все строки имеют следующий вид: или . Изменение сумм по строкам a и b не приводит к изменению сумм по столбцам в k-той строке. Операция корректна.

3.2. Найдется такая строка , для которой: Увеличение на координаты приводит к увеличению суммы координат по первому столбцу.

3.3. Найдется такая строка , для которой: Увеличение на координаты приводит к увеличению суммы координат по второму столбцу.

В вариантах 3.2. и 3.3. требуется модификация k-той строки. Рассмотрим подробно k-тую строку ячеек для варианта 3.2.

3.2.1. Все ячейки k-той строки (возможно кроме j-той) имеют две ненулевые координаты в одной строке. Операция корректна и не изменяет сумм по строкам.

3.2.2. Найдется такой столбец , для которого: Увеличиваем на , , уменьшаем на . При этом сумма координат по строке c увеличивается, по строке d уменьшается.

В случае варианта 3.2.2., принципиальным является вид ячейки i,l.

3.2.2.1. Увеличение на строки c приводит к увеличению первого столбца, как и требовалось для i-той строки ячеек. Операция корректна.

3.2.2.2. Увеличение на строки c приводит к увеличению второго столбца, но в i-той строке требовалось увеличить первый столбец. Операция не корректна. Этот вариант соответствует необходимому условию.

3.2.2.3. Изменение сумм по строкам c и d не изменяет сумм по столбцам в i-той строке. Операция корректна.

Вариант 3.3. рассматривается аналогично варианту 3.2. Кроме того, в варианте 3.2.2 мы поменяли суммы по строкам c и d. Его следует рассмотреть подобно варианту 3, взяв ячейку k,l вместо i,j.

В результате, все листья в дереве вариантов разбиваются на два конечных множества.

a. Для которых выполняется необходимое условие.

b. Для которых операция корректна. Точка v существует и принадлежит . Аналогично строится точка , но увеличивается второй столбец i-той строки. , u – середина отрезка, соединяющего v и w. Противоречие, u не является вершиной .

Теорема доказана.

2. Важнейшей составной частью линейного программирования является задача целочисленного программирования, т.е. нахождение решения в целых числах. От общей задачи она отличается, прежде всего, своей труднорешаемостью. В то время как для линейного программирования были найдены эффективные (полиномиальные) алгоритмы [5], задача целочисленной оптимизации не просто была охарактеризована как NP-полная, но и включена Карпом в список 21 основных NP-полных задач. Тем не менее, для специфических целевых функций эту задачу можно решить с помощью стандартных алгоритмов линейного программирования.

Теорема 2. Если целевая функция имеет вид:

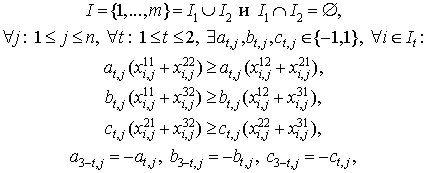
то на многограннике она принимает свой максимум в целой вершине.

Доказательство. Проведем доказательство для частного случая:

Предположим, что целевая функция принимает свой максимум в нецелочисленной вершине u. Для нее выполнено необходимое условие для нецелочисленных вершин (теорема 1).

	0
0
---	---

Ячейка i,j имеет вид: где

0
	0
---	---

Ячейка k,j имеет вид: где

Пусть для ячейки i,j: Тогда для k,j соответственно:

Без ограничения общности, будем считать, что , в противном случае вместо ячейки k,j, следует рассмотреть ячейку i,j.

x	y
z	t
---	---

Построим точку по вершине u, заменив ячейку k,j, на ячейку вида:

Для того чтобы замена была допустима и , система, задающая точку v, должна остаться совместной. В новой ячейке k,j сохраним старые ограничения по строкам и столбцам. Получим систему уравнений:

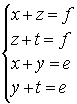
Решая систему, получим, что . Система примет вид:

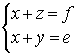
Имеем три неизвестных и два уравнения. Выберем .

e	0
f-e	e
--	--

Тогда, если новая ячейка k,j примет вид:

f	e-f
0	f
---	---

Если же новая ячейка k,j примет вид:

Следовательно, точка v существует и принадлежит .

Оценим целевую функцию в точке v. Строки a и b можно выбрать 3-мя способами.

1. . В данном случае, при замене, значение целевой функции уменьшится по переменным на , но увеличится по на . Т.к. для целевой функции выполняется неравенство ее значение не уменьшается.

2. . Значение целевой функции уменьшится по на , но увеличится на по и . За счет выполнения неравенства целевая функция не уменьшается.

3. . Аналогично пунктам 1 и 2.

В результате, значение целевой функции при переходе из вершины u в точку не уменьшается. Целевая функция будет принимать свой максимум также и в точке v. Причем, для данных i, j, k, l необходимое условие теперь не выполнено. Если v также является нецелочисленной вершиной , то аналогично можно перейти в точку w и далее, пока не перестанет выполняться необходимое условие для нецелочисленных вершин. Следовательно, целевая функция будет принимать свой максимум и в целочисленной вершине, что и требовалось доказать.

Доказательство для общего случая проводится аналогично. Возможны два варианта.

1. . В данном случае доказательство полностью повторяет рассмотренное.

2. . Тогда, вместо ячейки k,j следует рассмотреть одну из ячеек k,l или i,l, проведя для нее соответствующую замену.

Теорема доказана.

Теорема 2 открывают новые возможности в построении эффективных алгоритмов для задач комбинаторной оптимизации. Если для некоторой задачи X ее геометрической интерпретацией окажется задача целочисленного программирования на многограннике , и при этом целевая функция будет иметь описанный выше специфический вид, то для решения задачи X достаточно будет воспользоваться детально разработанными алгоритмами линейного программирования, высокая эффективность которых хорошо известна [5].

Литература:

1. Бондаренко В.А., Максименко А.Н. Геометрические конструкции и сложность в комбинаторной оптимизации. М.: ЛКИ, 2008. 184 с.

2. Деза М.М., Лоран М. Геометрия разрезов и метрик / Пер. с англ. Е. Пантелеевой и П. Сергеева. / Под ред. В. Гришухина. М.: МЦНМО, 2001.

3. Бондаренко В.А., Урываев Б.В. Об одной задаче целочисленной оптимизации// Автоматика и телемеханика, 2007 №6.

4. Дунаева О.А., Николаев А.В. Некоторые свойства релаксационного многогранника задачи 3-выполнимость // Математическое моделирование и краевые задачи. Самара. СамГТУ. 2008 г. С. 37-43.

5. Хачиян Л.Г. Полиномиальные алгоритмы в линейном программировании // ЖВМ и МФ. 1980. Т20, №1. С. 51-69.