Маслова С. В.

МГПИ им. М. Е. Евсевьева, каф. методики начального образования

Лысова В.Ф.

СОШ № 34, Саранск

Дивергентное решение текстовых задач

в курсе математики «Планета знаний»

Под дивергентными задачами понимаются такие задачи, которые имеют два и более верных варианта ответа. В начальном курсе математики в основном рассматриваются задачи конвергентного типа, что, к сожалению, не способствует развитию дивергентного мышления. Если рассматривать дивергентное мышление как самостоятельное, поисковое, оригинальное, продуктивное мышление, характеризующееся инверсионностью и дискретностью, то можно говорить об отсутствии динамики развития данного вида мышления. В дальнейшем это может привести к тому, что из младшего школьника вырастет абсолютно нетворческий человек.

По мнению Дж. Гилфорда, определившим дивергентное мышление в психологии, основанием данного вида мышления является порождение множества решений на основе однозначных данных. Человек в окружающем мире каждый день сталкивается с ситуациями, выход из которых далеко не однозначен. Большую часть психологических проблем, на сегодняшний день, мы имеем по той причине, что привыкли считаться с единственно возможным решением любой задачной ситуации.

Если младшему школьнику показать возможность получения несколько верных ответов на предложенную задачную ситуацию, то это будет способствовать уничтожению ненужных стереотипов мышления, развитию видения различных решений возникающих проблемных ситуаций. Мы сможем впоследствии иметь дело с глубоко и неоднозначно мыслящей творческой личностью.

Рассмотрим несколько дивергентных задач, представленных в учебнике математики за 1 класс по программе «Планета знаний» [1; 87].

Из каких фигур можно сложить прямоугольник?

Задача имеет несколько верных ответов, но, к сожалению, чаще всего мы останавливаемся лишь на одном: попарно объединенные многоугольники. В результате имеем дело с конвергентным решением дивергентной задачи:

Необходимо предоставить детям простор для нахождения других вариантов комбинации предложенных многоугольников. В качестве правильных ответов могут выступать следующие решения:

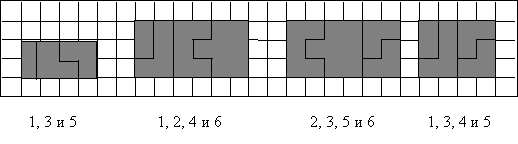
В конце концов, можно попробовать объединить все предложенные фигуры. Ответ также будет верным:

Не всегда дивергентная задача имеет дивергентное решение в практике обучения, не всегда мы видим дивергентную задачу в тексте учебника. Но иногда попадаются задачи, формулировка заданий которых уже говорит о неоднозначности их решения:

Наберите 50 очков разными способами. Записывайте суммы по очереди. Следите, чтобы равенства не повторялись.

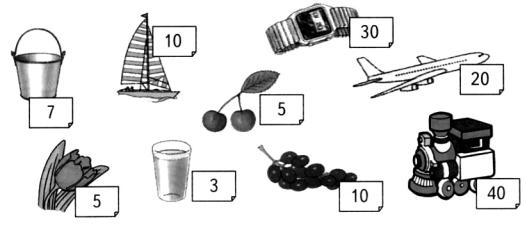
Замечательно, если учащиеся смогут показать все возможные варианты ответов:

30+20=50	30+10+5+5=50
40+10=50	30+10+7+3=50
40+5+5=50	30+7+3+5+5=50
40+7+3=50	20+10+10+5+5=50
30+10+10=50	20+10+10+7+3=50

В противном случае, необходимо строить работу над задачей таким образом, чтобы дети увидели и записали различные решения.

Но подобных заданий недопустимо мало в учебниках математики для начальных классов. В связи с этим нельзя говорить о целенаправленном развитии дивергентного мышления в процессе начального обучения математике.

Литература

1. Башмаков, М. И. Математика: учебник для 1-го кл. четырехлет. нач. шк.: В 2 ч. Ч.2 / М. И. Башмаков, М. Г. Нефедова. – М.: АСТ: Астрель, 2005. - 135 с.