Технические науки / 4. Транспорт

Куропятник А. С.

Днепропетровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, Украина

Уточнение к моделированию кривой провисания
несущего каната маятниковой подвесной дороги

         Несущий канат является одним из важнейших элементов конструкции двухканатных подвесных дорог, поскольку во время движения вагонов (вагонеток) воспринимает всю весовую нагрузку последних, а также собственный вес, который, учитывая диаметр каната (45 мм и более) и существенные длины пролетов современных дорог, весьма значителен. Принимая во внимание отсутствие каких-либо дублирующих элементов (как, например, дополнительный канат в тяговой системе маятниковых пассажирских подвесных дорог), становится очевидной важность высокой точности расчета несущего каната на прочность с целью предотвращения его обрыва в процессе эксплуатации.

         Основой методик проектного расчета канатных систем подвесных дорог являются эмпирические зависимости [1], сформулированные десятки лет назад на основании результатов лабораторных исследований и обобщения накопленного к тому времени опыта строительства и эксплуатации. Однако, учитывая изменение основных характеристик дорог в части повышения длин и уклонов пролетов, а также увеличения вместимости вагонов, возникает вопрос о необходимости пересмотра применяемых математических моделей с целью их уточнения. Принимая во внимание современный уровень развития компьютерной техники, становится целесообразным проведение аналитического моделирования, сочетающего в себе основные законы механики, применительно к решению задачи определения прочности каната.

         В основание аналитических методов исследования нагруженности несущего каната полагаются зависимости теории гибких нитей (раздел, описывающий провисание нитей с малыми стрелами) [2]. При этом считается, что кривая провисания каната под действием собственного веса – парабола, а под действием веса вагона – сочетание двух прямых отрезков, пересекающихся в точке приложения сосредоточенной силы (веса) [3, 4]. Недостатком такой теории является существенное снижение точности математической модели при приближении вагона к опорам, что обусловлено неучетом провисания по кривой одного из отрезков каната, имеющего значительную длину. Для устранения такой неточности будем считать, что отрезки каната по обе стороны от точки приложения сосредоточенной силы являются параболическими
(рис. 1).

Рис. 1. Кривая провисания несущего каната под действием собственного веса и веса вагона

         Из теории гибких нитей следует, что уравнение кривой провисания несущего каната имеет вид:

                                                  ,                                              (1)

где  – координаты точки кривой;

       – угол наклона хорды пролета;

       – провисание каната в точке с координатой ,

                                                                                            (2)

       – длина пролета;

       – величина наибольшего провисания каната в рассматриваемом пролете, определяемая при .

         Такое уравнение соответствует нагружению каната лишь собственным весом. Влияние веса вагона на форму кривой провисания проявляется в увеличении провисания в точке приложения силы за счет выпрямления отрезков каната, что может быть учтено путем введения поперечного коэффициента  в формулу (2) [5]:

                                            .                                        (3)

         Поскольку степень выпрямления отрезков каната зависит от соотношения распределенной и сосредоточенной нагрузок, то поперечный коэффициент может быть определен как отношение натяжения каната в точке с координатой  () к натяжению в середине пролета (срединное натяжение ), что с учетом зависимостей теории гибких нитей позволяет записать следующее:

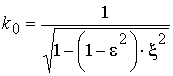                                              ,                                          (4)

где  – отношение монтажного натяжения к срединному;

       – коэффициент, учитывающий положение вагона в пролете.

         Монтажное натяжение определяется при отсутствии вагона в пролете, что соответствует провисанию каната по параболе:

                                        ,                                    (5)

где  – погонный вес каната;

       – относительное провисание каната.

         Величина  может быть определена разложением на составляющие: вертикальную  и горизонтальную . При этом

                                                  .                                              (6)

         Составляющие срединного натяжения могут быть определены из условия статического равновесия каната. Учитывая при этом особенности размещения вагона в пролете, имеем:

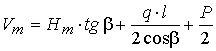                                          .                                      (7)

         Из выражения (4) видно, что при расчете срединного натяжения () , поэтому величина  может быть определена из выражения:

                                                                                          (8)

при условии .

         На основании выражения (6) получим:

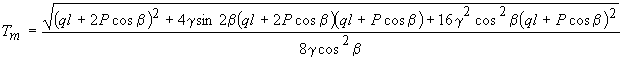  (9)

         Введя коэффициент дополнительной нагрузки (вес вагона по сравнению с собственным весом каната)

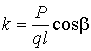                                                       ,                                                 (10)

получим выражение для определения параметра :

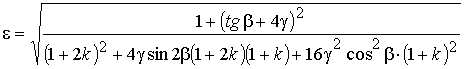                 .           (11)

         Сочетание выражений (1), (3), (4), (11) образует уточненную математическую модуль кривой провисания несущего каната, которая под действием веса вагона переходит из квадратичной (при действии лишь собственного веса каната) в параболу высшего порядка.

         Для оценки существенности выполненного уточнения рассмотрим влияние изменения формы кривой провисания на статическое усилие растяжения в канате, являющееся определяющей величиной в методике проектного расчета и выбора несущего каната. Указанное усилие может быть определено по формуле:

                                                   ,                                             (12)

где  – горизонтальная составляющая усилия;

       – угол наклона касательной к кривой провисания каната в точке приложения веса вагона (см. рис. 1).

         Из условия статического равновесия каната следует:

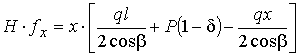                                  ,                            (13)

где  – относительное положение вагона в пролете.

         Принимая во внимание результаты выполненного выше математического моделирования, получим:

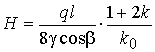                                                .                                          (14)

         В соответствии с разработанной математической моделью уравнение кривой провисания несущего каната имеет вид:

                                       ,                                 (15)

на основании чего определяем угол  по зависимости:

                                                        .                                                  (16)

         Окончательное выражение для определения угла  имеет вид:

                           .                     (17)

         Результаты сравнительного анализа метода 1, рассмотренного в работе [4] и основанного на допущении прямолинейности отрезков каната, и разработанной математической модели (метод 2) представлены на рис. 2. Анализ кривой погрешности расчетов по методу 1 указывает на то, что данный метод является достаточно точным с инженерной точки зрения и возможности его применения в практике проектирования канатных дорог в большинстве случаев, однако с приближением вагона к опорам ( и ) погрешность резко возрастает. Определенные по такому методу усилия в канате существенно больше действительных, на что указывает отрицательность погрешности, рассчитанной по формуле:

                                                 ,                                           (18)

где  – значения усилия растяжения каната, определенные по первому и второму методам соответственно.

Рис. 2. Результаты сравнительного анализа методик расчета несущего каната

         Это указывает на неоправданно высокий запас прочности, выражающийся в увеличении диаметра каната или его выборе из более прочной (и более дорогой) группы, который не только негативно сказывается на величине затрат на сооружение и дальнейшее обслуживание дороги, но и обуславливает появление дополнительной нагрузки за счет увеличения веса каната, которая не является полезной. Прослеживая влияние описанного явления в пределах канатной системы дороги, следует также отметить, что увеличение усилия растяжения несущего каната повышает нагруженность тягового каната. Это влечет за собой аналогичные несущему канату дополнительные финансовые затраты, а также негативно влияет на работу привода.

         Исходя из выше сказанного можно сделать вывод о целесообразности использования разработанной математической модели при проведении исследований канатных систем маятниковых подвесных дорог и их проектном расчете при условии использования средств автоматизированного проектирования.

Литература

         1. Олехнович А. И. Рациональные области применения пассажирских канатных дорог как средства городского транспорта // Труды ВНИИПТМАШ, 1969, №1. Исследование канатных дорог. – С. 3-43.

         2. Беркман М. Б. и др. Подвесные канатные дороги. – М.: Машиностроение, 1984. – 264 с.

         3. Прочность, устойчивость, колебания. Справочник в 3т. Т. 1 / Под общ. ред. Биргера И. А., Пановко Я. Г. – М.: Машиностроение, 1968. – 831 с.

         4. Горячев Ю. К., Куропятник А. С. Исследование влияния собственного веса на усилие в несущем канате маятниковой пассажирской подвесной дороги // Материали за IV Международна научна практична конференция «Научно пространство на Европа – 2008». Том 26. Технологии. – София: «БялГРАД-БГ» ОДД, 2008. – С. 71-77.

         5. Zweifel O. – Internationale Berg und Selilbahn – Rundschau, 1959, №2 / по Дукельский А. И. Подвесные канатные дороги и кабельные краны. – М.-Л.: Машиностроение, 1966. – 483 с.