O. Semenova, A. Semenov, O. Wojciechowska

Vinnytsya National Technical University

Realization of ternary minimum and maximum logic operations using parametrons

Modern systems of automatics and computing are being developed using logic algebra, not only binary one, but also multi-valued those. So, it is very important to define the most convenient type of logic for a system.

The multi-valued logic has some advantages then using in complex systems. The more logic values a system has, the higher quick-action it has. But the less logic values a system has the higher noise stability it has. So, the compromise between quick-action and noise stability can be achieved by using ternary logic [1].

In order to decrease a number of interconnections we propose to use the pulse-phase information coding method [2].

A pulse-phase element is the parametron. It works acocording to majority logic [3]. But the parametron has a disadvantage: its complexity increases as increases a number of logic levels. That is why in order to simplify implementation of ternary logic operations using the parametron we will use so called double wire logic.

Thus, an every logical value is presented as two phase shifts: one on the first wire and other on the second wire.

According to it, we propose the next coding.

A logical “0” corresponds to “0” and “0” phases.

A logical “1” corresponds to “0” and “π” phases.

A logical “2” corresponds to “π” and “π” phases.

So, one pulse-phase element consists of two three-input parametrons. A block diagram of the proposed phase ternary logic element is presented at fig.1.

This element operates according to table 1.

The first inputs give.

The second inputs give .

The outputs gives .

The auxiliary inputs give .

Table 1. Operation of the phase ternary logic element

First inputs		Second inputs		Auxiliary inputs		Outputs
x11	x21	x12	x22	y1	y2	z1	z2
0	0	0	0	0	0	0	0
0	0	0	π	0	0	0	0
0	0	π	π	0	0	0	0
0	π	0	0	0	0	0	0
0	π	0	π	0	0	0	π
0	π	π	π	0	0	0	π
π	π	0	0	0	0	0	0
π	π	0	π	0	0	0	π
π	π	π	π	0	0	π	π
0	0	0	0	π	π	0	0
0	0	0	π	π	π	0	π
0	0	π	π	π	π	π	π
0	π	0	0	π	π	0	π
0	π	0	π	π	π	0	π
0	π	π	π	π	π	π	π
π	π	0	0	π	π	π	π
π	π	0	π	π	π	π	π
π	π	π	π	π	π	π	π

Let be some ternary function of , so that

,
where are variables, is a constant.

For the ternary minimum operation we have:

.

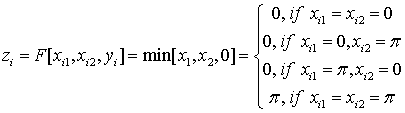For the ternary maximum operation we have:

.

In order to simplify the description we propose to use a matrix.

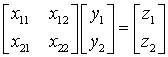
For the ternary minimum operation we have:

,

For the ternary maximum operation we have:

, .

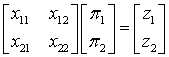So, we have proposed to build up the ternary minimum and maximum elements on parametrons. These elements work on double wire logic. Also we have proposed the pulse-phase information coding method and the matrix description.

References

1. Ëûñèêîâ Á.Ã. Àðèôìåòè÷åñêèå è ëîãè÷åñêèå îñíîâû ÝÖÂÌ. – Ìèíñê: Âûøýéøàÿ øêîëà, 1974. -264ñ.

2. Ìîë÷àíîâ À.À., Âîëêîãîí Â.Ï., Ëîçà Þ.Õ., ßëîâåãà Ã.È. Ïðîåêòèðîâàíèå ìíîãîôóíêöèîíàëüíûõ èíòåãðàëüíûõ ñõåì. –Ê.: “Òåõí³êà”, 1984. – 143ñ.

3. Êíîððå Ã.Ê., Òóçîâ Â.Ì., Øóð Ã.È. Ôàçîâûå è ÷àñòîòíûå èíôîðìàöèîííûå ÑÂ× ýëåìåíòû. –Ì.: Ñîâ. ðàäèî, 1975. –352ñ.