Д.т.н. Ободан Н.И., к.ф.-м.н. Громов В.А.

Днепропетровский национальный университет им. О. Гончара

Сведение уравнений нелинейной теории оболочек к последовательности систем одномерных интегро-дифференциальных уравнений

Аналитическому исследованию и численному анализу поведения решения уравнений нелинейной теории пологих оболочек посвящено значительное число исследований [1], что объясняется важностью тонкостенных конструкций для различных областей современной науки и техники. Экспериментально и теоретически установленная [2] существенная зависимость нагрузок потери устойчивости от внешних возмущений обуславливает необходимость выхода за пределы распространённого в инженерной практике метода конечных элементов и построения множества ветвей решения соответствующей нелинейной краевой задачи с последующим анализом областей существования различных типов решений по уровню нагрузки и по уровню развивающихся прогибов.

В настоящей работе предлагается метод вариационно-итеративного разделения переменных решения нелинейных краевых задач теории пологих оболочек. В качестве исходных разрешающих соотношений будем использовать соотношения, определяющие обобщённые решения нелинейной теории пологих оболочек [1].

Решение данной нелинейной краевой задачи представляется в виде

, ,

где – формальный малый параметр, функции и должны удовлетворять соответствующим граничным условиям.

Такое же представление используется для функций и :

, .

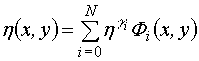Выделяя слагаемые при одинаковых степенях , можно получить последовательность соотношений для определения : в уравнения для определения входят ,…,,.

В частности, уравнения для начального приближения () и первой поправки ( ) принимают вид:

:,

;

:

,

,

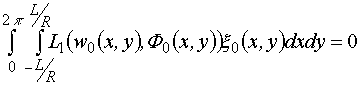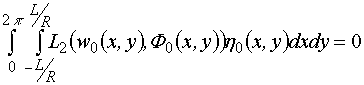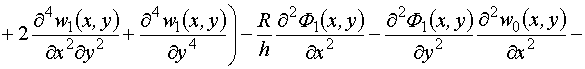
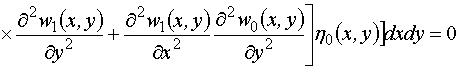где под операторами и понимаются операторы уравнений нелинейной теории оболочек.

Решение каждого из построенных уравнений ищется в классе функций, представимых в виде произведения функций одной переменной . Соответственно для функций, входящих в разрешающие соотношения можно получить следующие представления:

, , , .

Здесь функции , , , – дифференцируемые необходимое число раз произвольные функции одной переменной.

Полагая

, ,

и перебрасывая производные, в силу произвольности функций , , можно получить соотношения, связывающие неизвестные функции , , , . В частности, для данные соотношения принимают следующий вид (индекс 0 опущен):

,

.

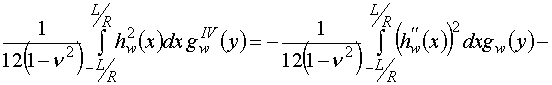
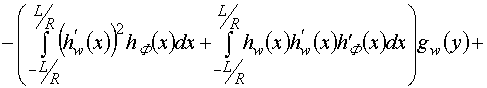
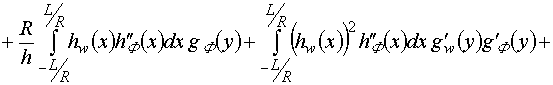
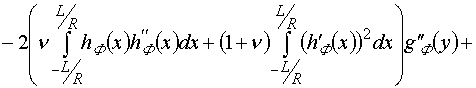
Литература:

1. Ворович И. И. Математические проблемы нелинейной теории пологих оболочек. – М.: Наука, 1989. – 376 с.

2. Красовский В. Л. Качество тонкостенных цилиндров и пусковые механизмы их выпучивания при продольном сжатии // Theoretical Foundations of Civil Engineering Polish-Ukrainian Transactions, Vol. 2, Warsaw, June 2002, – P. 696-715.