К.ф.-м.н. Адлуцкий В.Я.

Днепропетровский национальный университет, Украина

РАСПРОСТРАНЕНИЕ ТРЕЩИН В ОБОЛОЧКАХ С ОТВЕРСТИЯМИ

Постоянно возрастающие требования к надежности современной техники обусловливают необходимость разработки расчетных методик, учитывающих наличие изначально существующих или  возникающих и развивающихся в процессе эксплуатации механических повреждений различной природы, таких как расслоения, пробоины, трещины и т.п. Своевременная диагностика таких повреждений, прогнозирование их дальнейшего поведения в режиме реального времени и оценка их влияния на работоспособность детали и конструкции в целом являются насущными проблемами современной науки о прочности. 

Практически в любых современных технических решениях используются тонкостенные конструктивные элементы в силу присущего им оптимального сочетания жесткостных и весовых характеристик, поэтому анализ влияния повреждений на прочностные свойства таких элементов является актуальной задачей, решению которой посвящено много работ (в частности, [1-3]). Диагностика повреждений может быть осуществлена различными способами, в частности, на основе методов искусственного интеллекта, например, с использованием нейросетевого подхода [4]. В результате локализации повреждения и идентификации его размеров и формы возникает вопрос о его дальнейшем поведении. Как известно, наличие повреждений в виде отверстий с угловыми точками является источником зарождения и развития трещин, возникающих во входящих углах отверстий. Для моделирования процесса разрушения может быть использована теория хрупкого разрушения Гриффитса [6-8], во многих случаях обеспечи­вающая получение достаточно точных результатов.

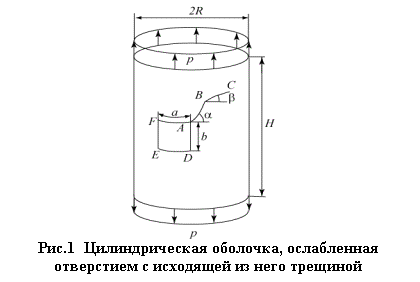
В постановке линейной механики разрушения рассматривается задача о возникновении и развитии трещин в круговой цилиндрической оболочке радиуса R,  высотой H и толщиной h, ослабленной прямоугольным отверстием с размерами a и b вдоль направляющей и образующей соответственно (рис.1), подверженной воздействию либо осевого растяжения равномерно распределенной по торцам нагрузкой интенсивности р, либо – внутреннего давления интенсивности q. В качестве источника образования трещины рассматривается либо зародыш трещины АВ длиной l, исходящий из вершины А под углом a к окружному направлению, либо сама угловая точка отверстия А (в этом случае точки А и B совпадают). Предполагается, что подрастание трещины происходит на величину  BC=Dl, а  направление роста определяется углом b к окружному направлению. Ставится задача определения направления развития трещины для указанных видов исходных повреждений и вариантов нагружения.

Моделирование поведения исследуемой оболочки с  повреждением осуществляется с помощью МКЭ в геометрически нелинейной постановке. Для дискретизации оболочки используется конечноэлементная сетка, состоящая из изопараметрических треугольных элементов оболочечного типа, позволяющих одно­временно учитывать мембранные и изгибные факторы. Нелинейный расчет осуществляется пошагово по мере роста параметра нагружения.

 

 

 

 

 

 

 

 

 

 

 

 

 


В качестве критерия разрушения выбирается энергетический критерий на основе инвариантного J-интеграла Черепанова-Райса [5-9]. Считается, что трещина начинает распространяться при условии , где  – предельное значение J-интеграла. В условиях идеально хрупкого разрушения величина J-интеграла представляет собой поток упругой энергии в вершину трещины, и величина  может трактоваться как вязкость разрушения. Обычно полагается, что  является константой для образцов определенной формы, изготовленных из конкретного материала. Как показывают исследования [10], для оболочки эта величина зависит от ее геометрии (в частности – от кривизны) и от длины трещины.

При решении рассматриваемой задачи, как в случае отсутствия зародыша трещины, так и при его наличии выбирается несколько возможных направлений распространения трещины. После вычисления J-интеграла, для каждого из таких направлений за истинное направление распространения трещины выбирается то, которому соответ­ствует экстре­мальное значение  J-интеграла. Для вычисления J-интеграла используется методика [10-11].

В качестве примера рассматривалась оболочка со следующими значениями параметров: ,. Параметры повреждений выбраны следующим образом: , при ,  при .

На рис.2 приведены примеры деформированного состояния оболочки, ослабленной прямоугольным отверстием и зародышем трещины АВ, исходящим из угловой точки А под углом . Для случая осевого растяжения угол, для случая внутреннего давления. Приведенные результаты демонстрируют качественные различия в характере деформи­рования оболочки с повреждениями в зависимости от вида нагружения. Так, для случая осевого растяжения в окрестности повреждения вдоль стороны FA имеет место выпучивание вовне, а вдоль стороны АD – в противоположном направлении.  Аналогичный эффект отмечен в литературе [3]. В случае внутреннего давления выпучивание происходит в противоположных направлениях по сравнению со случаем осевого растяжения. Этими отличиями обусловлено и несовпадение направлений развития трещин при рассматриваемых  видах нагружения.

Результаты расчетов на заключительном шаге процесса нелинейного решения приведены на рис.3.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Как следует из приведенных данных, в случае действия осевого растяжения приоритетным направлением развития трещины является окружное направление (), вне зависимости от того, имелся ли зародыш трещины и каково его направление. Такой вывод полностью согласуется с экспериментальными наблюдениями за направлением развития трещин, инициируемых зародышами указанных выше размеров. Аналогично, для случая действия внутреннего давления приоритетным направлением развития трещины является направление, близкое к , также вне зависимости от того, имелся ли зародыш трещины и каково его направление.

Следует отметить, что характер распределения значений J-интегралов для трещин различных направлений в процессе нелинейного решения оставался практически неизменным.  Это обстоятельство дает возможность судить об истинном направлении роста трещины по результатам расчета на достаточно ранних стадиях процесса нагружения.

Таким образом, характер  нагружения  тонкостенной конструкции с повреждением в виде отверстия с угловыми точками оказывает существенное влияние на возникнове­ние трещино­подобных дефектов  и направление их дальнейшего развития.

 

Литература:

1.    Гузь А. Н. и др. Разрушение и устойчивость тонких тел с трещинами / А. Н. Гузь, М. Ш. Ды­шель, Г. Г. Кулиев, О. Б. Милованова. – К., 1981. – 184 с.

2.    Дышель М. Ш. Исследование деформирования цилиндрической оболочки  в окрест­ности разреза при растяжении // Прикл. механика. – 1984. – Т.20,  №3. – С.108–110.  

3.     Дышель М. Ш.  Растяжение цилиндрической оболочки с разрезом // Прикл. механи­ка. – 1984.  – Т.20,  №10. – С.64–69.  

4.    Ободан Н.И., Адлуцкий В.Я., Киселев Э.М. Локализация повреж­дений в механичес­ких системах на основе нейросетевого подхода. – В кн.: Проблеми обчислювальної математики і міцності конструкцій: Збірник наукових праць / ДНУ. – Дніпропетровськ,  2005. – Вип.9. –  С.108-114.

5.    Качанов Л. М. Основы механики разрушения. – М., Наука, 1974. – 312 с.

6.    Керштейн И.М. и др. Основы экспериментальной механики разрушения. – М.: Изд-во Моск. ун-та, 1989. – 140 с.

7.    Партон В.З., Морозов Е.М. Механика упругопластического разрушения: Основы механики разрушения. ­– М.:Изд-во ЛКИ, 2008. ­– 352 с.

8.    Партон В.З., Механика упругопластического разрушения: Специальные задачи механики разрушения. – М.:Изд-во ЛКИ, 2008. ­– 192 с.

9.      Морозов Е.М., Никишков Г.П.  Метод конечных элементов в механике разруше­ния. –  М.: Изд-во ЛКИ, 2008. ­– 256 с.

10.    Ободан Н.И., Адлуцкий В.Я., Пацюк А.Г., Шерстюк Г.Г. Влияние кривизны тон­ко­стенных эле­ментов с тре­щинами на парамет­ры разрушения (теорети­ко-экспериментальное исследование). – Проблемы прочнос­ти. – №3, 2006. – С.75-85.

11.        Ободан Н.И., Адлуцкий В.Я. Потеря устойчивости цилиндрической обо­лоч­ки с трещиной как стартовый меха­низм разрушения. – Вісник ДНУ, №10/2,  2005,  – С.116-122.