Д.т.н. Ободан Н.И., к. ф.-м.н. Адлуцкий В.Я.

Дніпропетровський  національний  університет, Украина

 НЕЙРОСЕТЕВАЯ ДИАГНОСТИКА ПАРАМЕТРОВ

НЕСКВОЗНОЙ ТРЕЩИНЫ В ПЛАСТИНЕ

 

В последнее время все более увеличивается число публикаций, посвященных использованию физических косвенных методов неразрушающего контроля повреждений в материале: ультразвуковое, акустическое, магнитное воздействие и т. п. Интен­сивно развиваются математические методы решения некорректных задач для идентификации повреждений [1, 2].

Развитие метода неразрушающего контроля с исполь­зованием методов искусственного интеллекта, и, в частности, нейронных сетей, находится на начальной стадии. Появились публикации, относящиеся к сфере металлургии и машиностроения, однако все опубликованные методы базиру­ют­ся на простейших моделях или используют статистические данные, как правило, весьма противоречивые с точки зрения причин разрушения. Следует отметить, что решение методом нейросетевого управления обратных задач вообще, а тем более – для деформируемых тел, для которых эти задачи плохо обусловлены, представляет большие трудности. В литературе до сих пор практически отсутствуют сведения об использовании нейронных сетей в соче­та­нии с моделями механики сплошных сред.

Целью данной работы является построение и реализация алгоритма диагностики параметров несквозных трещин в тонких пластинах по результатам измерений перемещений в дискретных точках поверхности с использованием многослойных нейронных сетей на основе персептрона.

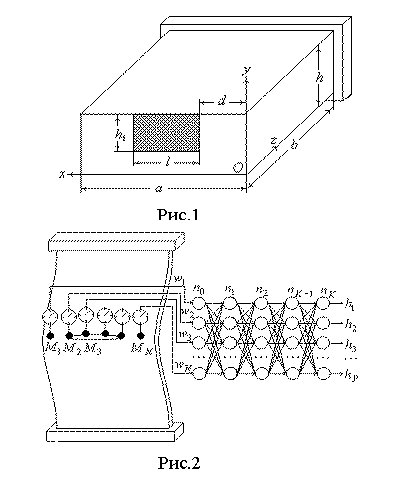
Прямая задача о напряженно-деформированном состоянии тонкой пластины, содержащей несквозную трещину, решается с помощью МКЭ. Рассматривается тонкая прямоугольная пластина (рис.1) длиной 2b, шириной a и толщиной h, центральное сечение которой (z=0) ослаблено несквозной трещиной прямоугольной формы длиной l и глубиной . Трещина расположена на расстоянии d от боковой поверхности. Пластина жестко защемлена по торцам и растянута на незначительную величину d так, чтобы в ней не возникли остаточные напряжения. Наличие трещины обусловливает изгиб пластины, который фиксируется индикаторами в дискретных точках поверхности, на которую выходит трещина (рис.2). Задача состоит в том, чтобы по значениям измеренных прогибов определить длину, глубину и положение несквозной трещины в центральном сечении пластины.

Для решения поставленной задачи применяется метод многослойных нейрон­ных сетей (МНС). Для обучения МНС используются решения прямой задачи механи­ки деформируемого тела для пластины с несквозной трещиной в центральном сечении, расположение и размеры которой варьируются. Решение прямой задачи строится на основе МКЭ путем разбиения пластины на трехмерные восьмиузловые изопараметрические конечные элементы  с узла­ми , где Q – общее число конеч­ных элементов, T – общее число узлов конечноэлементной сетки. С целью локализации трещины вводится разбиение цент­раль­ного сечения пластины z=0 на зоны  возможного расположения трещины. Информа­ция о нормальных перемещениях пластины с несквозной трещиной g формируется в точках съема информации Mi, ,

равномерно распреде­ленных по лицевой поверхности пластины в ее центральном сечении.

Для каждой трещины вектор переме­щений в точках съема информации  (где – нормальное перемещение в точке  в глобальной декартовой системе координат) пред­ставляет собой сово­куп­ность входных параметров МНС. В качестве вектора выходных параметров служит вектор H, определяющий зону локализации трещины, , где

                                             .

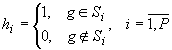Обу­чающая последо­вательность ,   состоит из r образцов.

Используется полносвязная МНС на основе персептрона, в которой каждый базовый элемент l-го слоя  передает свой входной сигнал с определенными весовыми коэффициентами всем нейронам следующего (l+1)-го слоя. Связи между базовыми элементами в слое отсутствуют. Обозначим  – число базовых элементов во входном слое,  – число базовых элементов в l-м скрытом слое, – число базовых элементов в выходном слое. С учетом структуры входного и выходного векторов очевидно, что . Выходной сигнал i-го базового элемента в l-м слое МНС вычисляется в виде

,

где  – весовой коэффициент связи, идущей от базового элемента с номером j к базовому элементу с номером i;  – активность i-го элемента в слое l; – весовой коэффициент, связанный с элементом смещения в (l–1)-м слое, значение активности которого = +1 для всех ; f(х)  – функция активации, которая в данном исследовании принята в виде гиперболического тангенса.

Среднеквадратичная ошибка наблю­да­емого сигнала в выходном слое для s-го образца равна 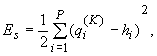 а общая ошибка для всей последовательности образцов .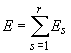

Для управляемого обучения МНС, в процессе которого веса  корректируются с целью минимизации ошибки E, применяется алгоритм обратного распространения ошибок [3], использующий два потока в сети: прямой поток от входного слоя к выходному и обратный – от выходного слоя к входному. Минимизация ошибки осуществляется методом градиентного спуска. Начальные значения весовых коэффициентов МНС формируются случайным образом. С целью недопущения «перетренировки» МНС, при которой сеть слишком хорошо повторяет учебные данные и не позволяет новым экземплярам  достаточно далеко отклоняться от них, процесс обучения сочетается с периодическим пропусканием через сеть набора тестовых данных. Обучение продолжается пока общая ошибка тестовых данных уменьшается, и прекращается, как только она начинает расти. Тестовые данные не предъявляются сети в качестве учебных.

Численные эксперименты осуществлялись с помощью пакета программ, реализу­ющих конечноэлементное решение прямых задач, генерацию обучающих и тестовых наборов данных, рандомизацию порядка их компонентов, построение, обучение и тестирование МНС. Строились МНС с различным количеством скрытых слоев и базовых элементов в этих слоях.

Рассматривались пластины со следующими значениями геометрических параметров: a=70 мм, b=175 мм, h=0,23 мм. При этом геометрические параметры трещин изменялись в следующих пределах:   . Типичный характер напряженно-деформированного состояния пластины с несквозной трещиной g при d=0,1a; l=0,12a;  приведен на рис.3, где линиями уровня обозначены эквивалентные напряжения (представленные в кг/мм2) в окрестности трещины. В данном случае пластина с несквозной трещиной моделируется с использованием сетки из 15000 конечных элементов со сгущением их к центральному сечению. По толщине пластины

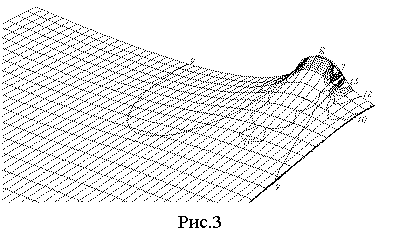
располагается 8 слоев конечных элементов.

В рассматриваемом случае максимальное нормальное перемещение пластины достигается в центре трещины и составляет 0,0026 мм. Выпучивание пластины происходит в сторону поверхности, на которую выходит трещина. Для любого другого расположения трещины напряженно-деформированное состояние пластины в ее окрестности остается качественно подобным приведенному на рис.3.

Обучение МНС производилось методом обратного распространения ошибок с использованием обучающих наборов данных, содержащих от r=144 до r=180 образцов, упорядоченных случайным образом. Каждый образец являлся результатом решения прямой задачи для пластины с несквозной трещиной определенной длины и глубины, расположенной в одной из зон локализации Si. Число зон локализации P варьировалось от 4 до 8, а число точек съема информации N – от 11 до 22. В качестве тестовых данных, используемых в процессе обучения, формировалась десятипроцентная выборка из обучающего набора. На этапе тестиро­вания настроенной МНС использовались двадцатипроцентные выборки из обуча­ю­щих наборов данных, не предъявлявшиеся при обучении.

Способность к обобщению построенных МНС существенно зависела от числа и расположения точек съема информации. Например, использование точек съема информации, расположенных вне окрестности трещины, не позволяло произвести настройку МНС с достаточной для практики точностью, что связано с плохой обуслов­ленностью исход­ной задачи и малой репрезентативностью наборов точек съема информации, удаленных от трещины. Наиболее эффективным оказалось расположение точек съема информации на лицевой поверхности пластины в ее центральном сечении (рис.2).

Результаты расчетов с варьированием количества скрытых слоев МНС показали, что сети с бόльшим количеством скрытых слоев обладают более высокой способ­ностью к обобщению, однако чрезмерное увеличение их числа (более 4), существенно замедляет процесс обучения из-за большого объема вычислений. Существенное влияние на обучение МНС оказывало выбираемое количество зон локализации трещины:  например, рассмотрение четырех зон:

 позволяло настроить МНС на 100%-е получение правильных тестовых решений, тогда как увеличение числа зон уменьшало число правильных результатов при тестировании до 85-90%. Попытки идентификации значений параметров трещин, а не зон их расположения, оказывались неуспешными, поскольку на стадии обучения не удавалось достичь приемлемого уровня ошибки обучения. Вследствие этого, на этапе тестирования наиболее точно идентифицируемыми параметрами являлись глубина трещины и ее положение относительно оси симметрии поперечного сечения пластины, тогда как длина трещины иденти­фици­ровалась намного хуже.

В целом, решение рассматриваемой задачи оказалась намного более трудоемким, чем, например, задачи об идентификации сквозных отверстий-повреждений в тонких цилиндрических оболочках [4]. Если в последнем случае обучение МНС осуществлялось за несколько тысяч эпох, то для рассматриваемой задачи оно требовало нескольких сотен тысяч эпох. Причиной этого является особенность рассматриваемого типа повреждений, связанная с их локализацией в поперечном сечении достаточно тонкой пластины, что делает входные данные слабо отличающимися друг от друга. Соответственно, итерационный процесс имеет неустойчивый и к тому же весьма осциллирующий характер. Альтернативой являлось использование на определенных этапах итерационного процесса метода сопряженных градиентов, который обеспечивал монотонный характер сходимости.

Численная реализация предложенного подхода экспери­ментально подтвердила способность МНС служить средством определения наличия несквозных трещин в тонких пластинах.

 

Литература:

1.   Ободан Н.И., Богачев А.С., Шульга А.С. Диагностика механических систем по косвенным измерениям с помощью нейронной сети // Theor. Found. of  Civil Eng. XII. – Warsaw, 2004. – P.783-788.

2.   Головко В.А. Нейроинтеллект: Теория и применение. – Брест: БПИ, 1999. – 234 с.

3.   Хайкин С.  Нейронные сети. Полный курс. – М.: Изд. Дом "Вильямс", 2006. – 1104 с.

4.   Ободан Н.И., Адлуцкий В.Я., Соенко Д.С.  Локализация повреж­дений в механичес­ких системах на основе нейросетевого подхода. – IV Міжнародна науково-практична конференція “Мате­матичне та програм­не забезпечення інте­лек­туальних систем (MPZIS-2006)”,  Дніпропетровськ, 15-17 листопада 2006 р. Тези доповідей. –  С.116-117.