Карачун В.В., Мельник В.Н.

Национальный технический университет Украины “КПИ”

о природе воздействия акустической волны

на жидкофазный подвес

Анализ показывает, что упругие деформации не влияют на величину окончательного перемещения пузырька, так как величины ограничены, а остаточные деформации равны нулю, вследствие чего равны нулю и члены, им соответствующие.

Если функции не интегрируемы (в случае реальной жидкости), масса пузырька и деформации его поверхности не влияют на предельные перемещения. Этот вывод следует из факта отсутствия обобщенных масс пузырьков в выражениях для их предельных перемещений.

В том случае, когда деформации обоих тел упругие, главные центральные оси, а также их массы (моменты инерции) соответственно совпадают и окончательные перемещения пузырька и фиктивного тела (жидкости в отсутствие пузырька) равны между собой. Деформации фиктивного тела будут упругими, например, в случае плоской акустической волны, когда все частицы жидкости перемещаются на одно и то же расстояние.

Отсутствие предельного перемещения при линейно-упругом и вязкоупругом подвесе гироузла означает наличие незатухающих колебаний.

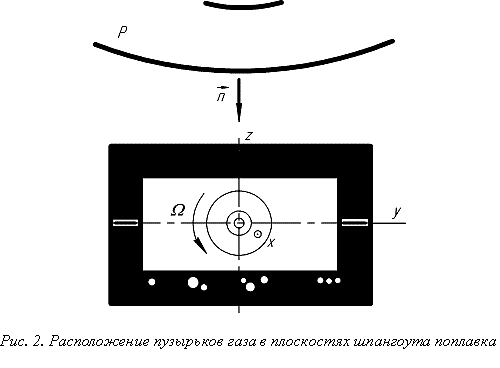
Пусть в жидкости, вследствие воздействия либо ударных, либо тепловых факторов (или тех и других одновременно), возникли пузырьки газа (рис. 2).

Проанализируем природу появления момента гидростатических сил, обусловленных перемещением пузырьков внутри объема жидкости.

В исходном состоянии силы веса гироузла и архимедова сила направлены по одной прямой в противоположные стороны, так что имеет место равенство

Образование пузырьков, естественно, приведет к параллельному смещению вектора и возникновению возмущающего момента относительно выходной оси . Величина этого момента определится соотношением

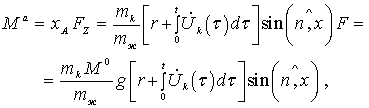(1)

где – соответственно массы го пузырька в фиксированной плоскости шпангоута, например, ДУСУ, вытесненной поплавком жидкости и жидкофазной части подвеса; ускорение свободного падения;

статический момент массы пузырька.

Если пузырек не перемещается то выражение (1) упрощается –

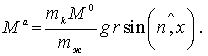(2)

Здесь предполагается, что радиус пузырька намного меньше радиуса поплавка, то есть

Если в плоскости шпангоута находится пузырьков, формула (1) приобретает вид –

. (3)

Предположим, что пузырьки газа собираются в плоскостях шпангоутов (рис. 2). Тогда в окончательном виде получаем:

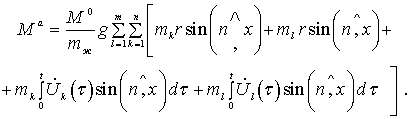(4)

Если учитывать радиус пузырька, считая его достаточно большим, тогда можно уточнить формулу (4):

(5)

Как уже было сказано, акустическое излучение достигает максимальных значений во время старта, к примеру, РН. С увеличением высоты полета, то есть при движении ракеты в области пониженного давления, эта величина существенно снижается. Поэтому можно принять полный импульс акустического давления конечным по величине. В этом случае, образовавшиеся пузырьки газа переместятся на фиксированную величину и остановятся после прекращения действия акустического излучения.