Технические науки. Металлургия

К.т.н. Досмухамедов Н.К.

Научно-производственная фирма «Консалтинг металл сервис», Казахстан

К вопросу теории и практики переработки промпродуктов и оборотных материалов свинцового производства

Изучение распределения металлов между продуктами металлургического производства является важнейшим вопросом теории и практики металлургических процессов, так как он, включая в себя извлечение металлов в полезный продукт и потери их с отвальным продуктом, определяет экономику и технологию процесса в целом. Определение термодинамического предела растворимости металлов в шлаках, как это было установлено в выше проведенных исследованиях, требует знания форм нахождения металлов в продуктах плавки и механизма их перехода из одной фазы в другую. При этом если в технической литературе имеется достаточное количество способов определения механических потерь металлов со шлаками, то определение растворенных потерь металлов со шлаками требует уточнения и проведения дополнительных экспериментальных исследований для каждого конкретного случая.

Так, за последние годы детально исследованы равновесия систем медь – шлак и медный штейн – шлак, определены зависимости меди в шлаках от различных факторов: температуры, окислительного потенциала газовой фазы (Р_О2), состава шлака, активности меди. Тем не менее, несмотря на обширный имеющийся материал, оставалось неясным, с чем связаны расхождения экспериментальных данных различных авторов: с различием условий проведения опытов или с погрешностями примененных методик и экспериментов. Ответы на эти вопросы были даны в работе [1]. На основании системного анализа имеющегося материала с единых позиций, авторами проведена проверка согласованности экспериментальных данных и построена термодинамическая модель, описывающая оксидную растворимость меди в шлаке.

Значительно хуже обстоит дело по изучению растворимости свинца в шлаках. Определению растворимости свинца в шлаках посвящено ограниченное количество работ. Можно отметить лишь несколько системных исследований [2,3], где на основании изучения равновесия свинец – шлак определяли растворенные потери свинца со шлаком. Данных по изучению растворимости меди и свинца из медно-свинцовых штейнов в шлак, за исключением работы [2], в технической литературе практически нет.

Ограниченность имеющегося экспериментального материала сильно сдерживает создание прогнозирующей термодинамической модели растворимости свинца в шлаках, аналогичной меди. Необходимость проведения дополнительных исследований и наработки экспериментального материала очевидна.

Экспериментальные исследования проводили с использованием сульфидных расплавов на основе сульфидов меди, железа, свинца переменного состава. Состав синтетического железосиликатного шлака фиксировался постоянным. Такой подход позволил уточнить механизм перехода меди и свинца из штейна в шлак и оценить влияние состава исходного сульфидного расплава на растворенные потери меди и свинца в шлаках. При этом основное внимание акцентировалось на количественное определение растворенных потерь меди и свинца в шлаке. Выбор состава исходных сульфидных сплавов проводился с учетом составов полиметаллических сульфидных материалов, получаемых на практике.

Экспериментальная часть.

Для определения растворимости цветных металлов в железосиликатном шлаке применен динамический метод, который позволяет определить потери меди и свинца со шлаком при контролируемых давлениях Ро₂ и Рs₂. Сущность метода заключается в том, что в равновесие со сложной газовой смесью – CO₂–СО–SO₂ заданного состава приводится система штейн-шлак.

Методика проведения экспериментов заключалась в следующем.

Навески медно-свинцового штейна и железосиликатного шлака помещаются в лодочку, которая ставится на специальную подставку, приготовленную из пеношамотного материала.

В работе [2] установлено, что при контакте штейна со шлаком, в результате растекания штейна за счет смачивания им шлака и капиллярного поднятия происходит увеличение механических потерь металлов со шлаком. Для установления растворенных потерь металла в шлаке необходимо устранить или свести к минимуму его механические потери. Это было достигнуто тем, что в проведенных экспериментах при нагреве исходной навески расплавленный шлак стекал к штейну. Далее подставка вместе с лодочкой загружается в кварцевый реактор, который снабжен патрубком для входа и выхода газовой смеси. В рабочую зону кварцевого реактора одновременно помещается от четырех до шести лодочек с исходной навеской. Перепад температуры по всей длине рабочей зоны минимален и составляет не более ±10º С от заданной температуры. Контроль температуры осуществляли термопарой ПП-1.

После загрузки лодочек, кварцевый реактор закрывался патрубком, после чего, на него надвигали силитовую печь, которую нагревали до необходимой температуры и выдерживали в течение необходимого времени. Подачу заранее приготовленной газовой смеси заданного состава начинали с момента нагрева печи. Расход газовой смеси в течение всего эксперимента оставался постоянным, и составлял 1 л/ч.

По истечении необходимого времени печь отключали. Подача газовой смеси в реактор прекращали в момент полного остывания печи. Далее печь отодвигали от кварцевого реактора и изымали подставки с лодочками. После разделения штейна и шлака их подвергали химическому анализу.

Состав исходного железосиликатного шлака, использованного при экспериментальных исследованиях, был постоянного состава и содержал, % мас.: 65,46 FeO; 30,8 SiO₂; 3,74 Fe₃O₄.

Синтетические медно-свинцовые штейны переменного состава готовили смешиванием заранее приготовленных чистых сульфидов меди, свинца и железа в строго рассчитанных количествах. Расчеты необходимого количества сульфидов вели исходя из того, чтобы в исходном штейне сумма содержания меди и свинца равнялась 30, 40, 50, 60, 70, 75 и 80 % мас., а их отношение менялось от 0,5 до 3,0. Навеска штейна во всех опытах была постоянной и равнялась 2 г., а шлака – 4 г. Ко всем штейнам было добавлено по 2 % мышьяка и сурьмы от веса исходного штейна. Выбранные составы исходных штейнов полностью покрывают область составов штейнов, получаемых на практике.

При проведении экспериментов очень важен выбор контролируемых значений Р_О2 и Р_S2, которые при прочих равных условиях должны соответствовать их значениям, принимаемым в условиях промышленного эксперимента. Для выбора контролируемых значений Р_О2 и Р_S2 нами были проведены дополнительные исследования по исследованию составов промышленных шлаков, полученных в условиях шахтной сократительной плавки свинцовых материалов.

После предварительного отделения сульфидной составляющей, пробы шлаков подвергали химическому, минералогическому и ЯГР методам анализа.
Химическим методом анализа определяли общее (Fe_общ.) и двухвалентное (Fe²⁺) содержание железа в шлаках. Содержание трехвалентного железа (Fe³⁺) рассчитывали по разнице: Fe³⁺ = Fe_общ. – Fe²⁺.

Минералогические исследования проб шлаков проводили на электронном микрозонде MS-46 фирмы «Камека». Установлено, что доля двухвалентного железа во всех исследованных пробах шлаков примерно постоянно и составляет 74-78 % от общего его содержания. Доля трехвалентного железа находится на уровне 15 % от общего содержания железа в шлаке.

ЯГР анализ проводили на спектрометре, где измерения проводили на порошковых пробах шлаков при комнатной температуре с целью определения наличия форм нахождения железа в шлаках.

Результаты трех независимых исследований проб шлаков показали хорошую сходимость. Содержание общего железа в исследованных пробах шлаков варьировало в незначительных пределах – 20-24 % мас. Изменение содержания Fe²⁺ в шлаках при этом составило 15-19 % мас. Содержание Fe³⁺ в шлаках варьировало в пределах 3-4 % мас. Установленное незначительное изменение содержания Fe²⁺ и Fe³⁺ в шлаках позволяет утверждать, что технологические параметры, влияющие на распределение металлов между продуктами плавки, в условиях ведения промышленных плавок оставались постоянными. Следовательно, можно предположить, что при шахтной сократительной плавке значения величин Р_О2 и Р_S2 также должны сохраняться на одном уровне.

На основании зависимости: lg (Fe³⁺/ Fe²⁺) = 0,196 lg P_O2 + 0,722, установленной в работе [4] и полученных результатов по содержанию Fe²⁺ и Fe³⁺ в шлаках были рассчитаны значения величины lg P_O2, для каждого состава шлака. Расчетами установлено, что величина lg P_O2 в условиях промышленных плавок менялась в узком интервале – от lg P_O2 = -9,2 до lg P_O2 = -9,9, где Р _O2 – величина парциального давления кислорода, атм. Это указывает на то, что при шахтной сократительной плавке величина Р_О2 находится практически на одном уровне. Задаваемое значение Р_О2 в условиях проведения опытов выбрано с учетом установленного расчетного значения.

Величины кислородного и серного потенциалов задавали выбором необходимого состава газовой смеси СО-СО₂-SО_2. При этом содержание SO₂ в газовой смеси составляло 17 %, что обеспечивало значение Р_S2, соответствующее условиям восстановительной атмосферы. Значения Р_О2 и Р_S2 во всех опытах оставались постоянными, и поддерживались на уровне: Р_О2 = 2,74*10ˉ⁴ Па и

Р_S2 = 1,45*10² Па.

Эксперименты проводились при температуре 1523 К.

Пробы штейнов и шлаков, после опыта, подвергались химическому анализу на содержание в них меди, свинца, мышьяка и сурьмы. Результаты экспериментальных исследований приведены в таблице.

Таблица. Расчетные значения коэффициентов распределения меди, свинца,

мышьяка и сурьмы между штейном и шлаком

№№ пп.	Содержание металлов в конечном штейне, % мас.				Состав конечного шлака, % мас.						Коэффициенты распределения металлов, LMe
	[Cu]	[Pb]	[As]	[Sb]	(Cu)	(Pb)	(As)	(Sb)	(FeO)	(SiO2)	LСu/10	LPb	LAs	LSb
1.	4,37	23,08	0,08	0,91	0,13	0,88	0,11	0,25	58,93	28,43	3,36	26,23	0,73	3,64
2.	11,2	19,4	0,22	0,89	0,14	0,58	0,13	0,24	64,03	28,31	8,0	33,45	1,7	3,7
3.	16,3	13,72	0,36	1,0	0,16	0,12	0,14	0,28	59,23	27,84	10,2	114	2,6	3,6
4.	19,04	9,5	0,47	1,01	0,19	0,23	0,15	0,28	63,16	28,29	10,02	41,3	1,8	3,61
5.	22,71	18,31	0,51	0,79	0,17	0,49	0,16	0,22	63,33	27,74	13,36	37,4	3,2	3,6
6.	24,9	13,85	0,63	0,89	0,2	0,13	0,18	0,25	64,2	27,89	12,45	106,5	3,5	3,56
7.	31,62	8,67	0,78	0,83	0,21	0,3	0,19	0,23	59,87	29,1	15,1	28,9	4,1	3,6
8.	26,32	23,45	0,61	0,6	0,18	0,91	0,18	0,17	65,36	28,7	14,62	25,8	3,4	3,5
9.	28,4	19,21	0,69	0,69	0,23	0,57	0,18	0,19	64,29	27,4	12,35	33,7	3,8	3,63
10.	29,87	28,63	0,73	0,42	0,22	1,34	0,19	0,12	63,83	28,05	13,58	21,4	3,84	3,5
11.	36,42	23,17	0,86	0,48	0,26	0,89	0,21	0,13	64,02	27,97	14,0	26,03	4,1	3,7
12.	39,07	19,42	0,9	0,57	0,28	0,58	0,21	0,16	60,73	29,54	13,95	33,48	4,3	3,56
13.	34,8	32,86	0,84	0,25	0,24	1,68	0,2	0,1	57,9	28,78	14,5	19,56	4,2	2,5
14.	38,1	28,57	1,15	0,31	0,27	1,33	0,24	0,09	62,87	27,97	14,1	21,48	4,8	3,4
15.	44,8	23,18	1,18	0,39	0,28	0,89	0,25	0,11	59,74	29,45	16,0	26,05	4,72	3,5
16.	48,74	22,8	1,16	0,35	0,3	0,86	0,19	0,1	61,83	28,64	16,25	26,5	6,1	3,5
17.	56,09	18,62	1,37	0,38	0,32	0,52	0,29	0,18	65,73	27,13	17,53	35,81	4,7	2,1
18.	62,3	13,47	1,46	0,44	0,33	0,11	0,32	0,12	62,87	28,05	18,9	122,5	4,6	3,66
19.	44,8	33,75	0,98	0,1	0,26	1,76	0,19	0,03	63,16	29,12	17,23	19,18	5,2	3,3
20.	48,72	27,92	1,23	0,22	0,28	1,28	0,26	0,06	62,49	29,47	17,4	21,81	4,7	3,66
21.	59,47	17,09	1,47	0,39	0,29	0,39	0,29	0,19	61,92	28,97	20,5	43,82	5,1	2,1

Обсуждение результатов.

Общий анализ экспериментальных результатов показывает, что содержание свинца в исходном штейне на оксидную растворимость меди оказывает лишь слабое влияние. В случае со свинцом, его растворимость в шлаке определяется как изменением отношения Cu/Pb, так и содержанием железа в штейне. В результате совместной математической обработки экспериментальных и промышленных данных получены следующие уравнения:

(Cu) = 0,199 + 3,118*10ˉ³[Cu] – 2,29*10ˉ³[Pb], r = 0,92; (1)

(Pb) = 0,431 + 0,011[Pb] – 1,127*10ˉ³[Fe] , r = 0,94. (2)

где r – коэффициент корреляции.

Высокое значение коэффициентов корреляции r = 0,92 и r = 0,94 свидетельствует о сильной связи между рассматриваемыми величинами. Нетрудно видеть, что растворимость свинца в шлаке падает с повышением содержания железа в штейне. Установленная количественная зависимость подтверждает оксидный механизм перехода свинца в шлак.

Для более точного прогнозирования растворимости меди и свинца в шлаке нами построены уравнения множественной корреляции, описывающие зависимость искомых величин от состава штейна. Полученные уравнения имеют следующий вид:

(Cu) = – 9,819 + 0,128 [Cu] + 0,113 [Pb] + 0,167 [Fe], r = 0,97; (3)

(Pb) = 5,734 – 0,07 [Сu] – 0,05 [Pb] – 0,09 [Fe], r = 0,98, (4)

где r – коэффициент множественной корреляции.

Уравнения (1) – (4) позволяют оценить влияние состава штейна на конечное содержание меди и свинца в шлаке и могут быть использованы для количественной оценки растворенных потерь металлов со шлаком на практике.

На следующем этапе исследований определяли коэффициент распределения металлов, который представлял традиционную задачу расчета исходя из отношения содержания металла в штейне к его содержанию в шлаке. Результаты рассчитанных значений коэффициента распределения меди, свинца, мышьяка и сурьмы сведены в таблицу.

На рис.1-4 показаны зависимости коэффициентов распределения металлов между штейном и шлаком от их содержания в штейне при постоянном значении давления кислорода и серы, а также температуры. Нетрудно видеть общую закономерность для меди и мышьяка – коэффициенты распределения повышаются с увеличением их содержания в штейне (рис.2, 4). Результаты по коэффициенту распределения этих металлов практически ложатся на прямую линию, при незначительном разбросе данных. Это свидетельствует о том, что в рассматриваемой системе механизм перехода меди и мышьяка в шлак описывается реакциями их окисления. При этом их потери со шлаком определяются оксидной формой растворимости в шлаках.

Обращает на себя внимание то, что коэффициент распределения свинца между штейном и шлаком плавно снижается с увеличением содержания свинца в штейне. Причем при низких концентрациях свинца наблюдается заметный разброс данных (рис.1).

Коэффициент распределения сурьмы с увеличением ее содержания в штейне меняется слабо, и находится практически на одном уровне (рис.3). Данное положение согласуется с выводами работы [3], где установлено, что в условиях восстановительной атмосферы переход сурьмы из штейна в шлак в основном обуславливается его переходом в шлак в виде Sb⁰.

Наблюдаемые на рис.1-4 зависимости неплохо описываются уравнениями, построенными в результате математической обработки экспериментальных данных, которые имеют вид:

L_Cu / 10 = 0,93 + 0,37 [Cu], r = 0,91; (5)

L_Pb = 45,23 – 0,69 [Pb], r = 0,77; (6)

L_As = 1,44 + 2,88 [As], r = 0,89; (7)

L_Sb = 2,96 + 0,74 [Sb], r = 0,74, (8)

где r – коэффициент парной корреляции.

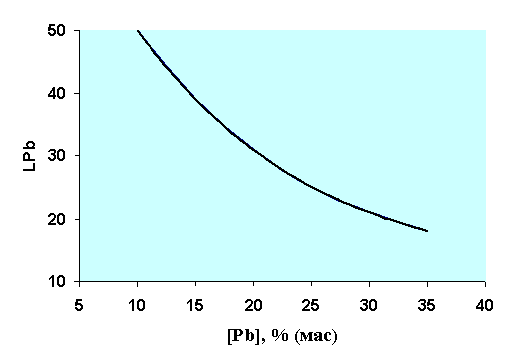
Рис.1. Зависимость коэффициента распределения свинца (L_Pb)

от его содержания в штейне, % (мас.)

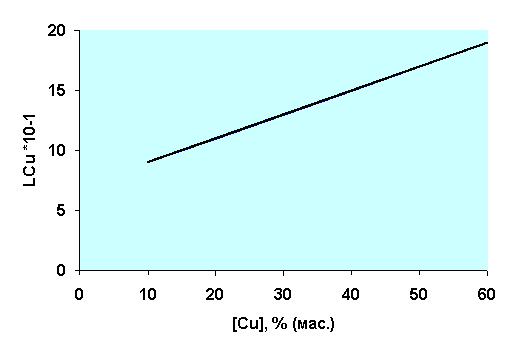
Рис.2. Зависимость коэффициента распределения меди (L_Cu*10^-1)

от ее содержания в штейне, % (мас.)

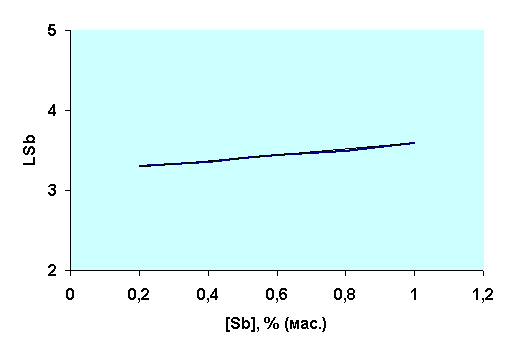
Рис.3. Зависимость коэффициента распределения сурьмы (L_Sb)

от его содержания в штейне, % (мас.)

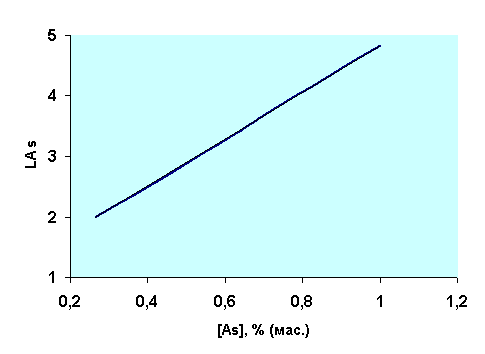
Рис.4. Зависимость коэффициента распределения мышьяка (L_As)

от его содержания в штейне, % (мас.)

Сравнительно высокие коэффициенты корреляции уравнений (5) и (7) указывают на сильную связь между рассматриваемыми величинами.

Коэффициенты корреляции уравнений (6) и (8) также указывают на сильную связь величин между собой. Относительно низкое значение коэффициента корреляции уравнения (8) для сурьмы объясняется спецификой механизма перехода сурьмы из штейна в шлак – в металлической форме.

Уравнение (6) описывает зависимость коэффициента распределения свинца для всего массива без учета отношения Cu/Pb. В тоже время установлено, что содержание растворенного свинца в шлаке существенно снижается при увеличении данного отношения. По-видимому, при учете отношения Cu/Pb можно было бы построить более точное уравнение. Обратный знак перед значением содержания свинца в штейне, полученное в уравнении (6) подтверждает направление кривой, показанной на рис.1.

Установленные закономерности для свинца подтверждают сложный механизм его перехода в шлак. В условиях опытов термодинамическая вероятность окисления сульфида свинца возможна по реакциям:

[PbS] + 3/2O₂ = (PbO) + SO₂, (9)

[PbS] + (FeO) = (PbO) + [FeS]. (10)

Протекание реакции (9) предпочтительнее (ΔG = −290552,2 Дж/моль), чем протекание реакции (10), для которой энергия Гиббса составляет

ΔG = – 85372 Дж/моль.

При равновесии системы константы этих реакций равны между собой. Следовательно, можно записать:

a_(PbO)*P_SO2 / a_[PbS]*P_O2³/² = a_(PbO)*a_[FeS] / a_[PbS]*a_(FeO). (11)

Учитывая, что в условиях опытов величины Р_О2 и Р_SО2 фиксированы решим левую часть выражения (11) относительно a_(PbO):

N_(PbO) = K1* N_[PbS], (12)

где - a_(PbO) и a_[PbS] заменено на произведение N_(PbO) *γ_(PbO) и N_[PbS]* γ_(PbS) ;

К1 – постоянная величина, К1 = К₍₉₎*Р_О2* γ_[PbS] / P_SO2* γ_(PbO).

С другой стороны, решение правой части выражения (11) относительно a_(PbO) позволяет записать:

N_(PbO) = K2* N_[PbS] / N_[FeS], (13)

где - активности заменены на произведение N*γ;

К2 = К₍₁₀₎* γ_[PbS]*N_(FeO)* γ_(FeO) / γ _[FeS]* γ_(PbO).

Из выражения (13) нетрудно видеть, что отношение N_PbS / N_PbO ≈ L_Pb обратно пропорционально содержанию железа в штейне - N_FeS. При увеличении содержания свинца в штейне содержание железа в нем уменьшается, что в свою очередь ведет к снижению коэффициента распределения свинца между штейном и шлаком. Обратный характер зависимости коэффициента распределения свинца от его содержания в штейне, показанный на рис.1, полностью подтверждает это положение.

Совместный анализ экспериментальных и промышленных результатов позволяет сделать ряд обобщающих выводов. В восстановительных условиях растворимость меди в шлаках, как в условиях эксперимента, так и в промышленных условиях определяется содержанием сульфида меди в штейне. Напомним, что в промышленных штейнах около 80 % меди, от общего ее содержания, присутствует в сульфидной форме. При этом механизм перехода меди из штей-на в шлак подчиняется традиционным закономерностям и определяется в основном оксидной ее растворимостью.

В случае со свинцом картина представляется более сложной. В промышленных штейнах свинец представлен в двух формах – в виде сульфида и в форме растворенного металла. В шлаках свинец обнаружен в форме оксида, сульфида и растворенного металла. Причем доля оксидной составляющей свинца в шлаке превалирует. Если исключить механические потери свинца в шлаках в виде его сульфида, а также долю свинца в виде растворенного металла, то снижения оксидных потерь свинца в шлаках можно достичь уменьшением концентрации сульфида свинца в исходном штейне. Это положение полностью подтверждают результаты практики. Вследствие повышенного содержания в штейнах сульфида свинца и свинца, растворенного в виде металла свинца, общее содержание последнего в шлаках остается высоким. Очевидно, что при шахтной сократительной, равно как и при любой свинцовой плавке на штейн нужно более четко оптимизировать состав получаемых штейнов с целью обеспечения минимальной растворимости свинца в нем и снижения содержания его сульфида.

Из вышеизложенного следует, что для снижения потерь свинца со шлаком необходимо, в первую очередь, минимизировать долю свинца, растворенного в штейне в виде металла, после чего влиять на снижение содержания сульфида свинца в штейне.

Литература

1. Васкевич А. Д., Сорокин М. Л. Модель оксидной растворимости меди в шлаках // Цветные металлы. 1982. № 7. С. 25-28.

2. Ванюков А. В., Зайцев В. Я. Шлаки и штейны цветной металлургии. М.:

Металлургия, 1969, с.408.

3. Володченко С.Н., Васкевич А.Д., Ванюков А.В. Исследование фазовых равновесий в системе Cu – Pb – S при 1473 К. – РЖ. Металлургия, 1982, №9, реф. 9А91.

4. Манцевич Н.М., Разумовская Н.Н. Мессбауэровское исследование форм

нахождения железа в шлаках // Цветные металлы. 1992. № 12. С. 15-19.