Технические науки 6

Соборницкий В.И., Павлюс С.Г., Апопий А.Г.

Украинский государственный химико-технологический университет

Соборницкая В.В.

Днепропетровский государственный университет железнодорожного транспорта

Коэффициент мощности и КПД трансформатора

Приводимая в литературе зависимость коэффициента мощности трансформатора ограничена качественным составом потребителя от активного до активно-индуктивного (Кривая 4,5 рис. 5). В работе теоретически обсуждена зависимость cos φ=f(β) при полном диапазоне изменения характера потребителя от идеального ёмкостного до идеального индуктивного.

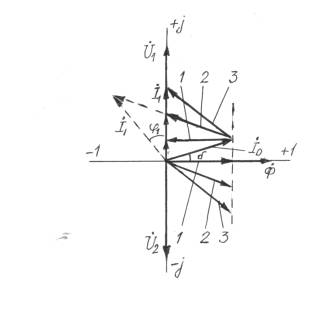
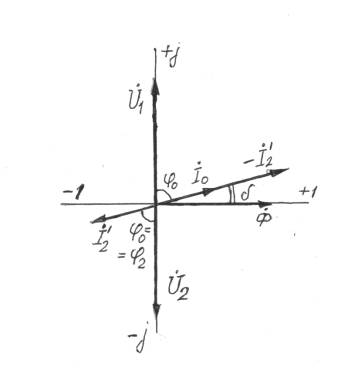
Рис. 1 . Векторная диаграмма для Рис. 2.Векторная диаграмма для

ёмкостной и активно-ёмкостной случая неизменного cos φ.

нагрузок.

На рис.1 приведены векторные диаграммы для идеальной ёмкостной нагрузки (вектор 1) и активно-ёмкостной (вектора 2 и 3) до значений коэффициента нагрузки, при котором зависимости cos φ=f(β) достигают максимальных значений. Было получено приближенное выражение для указанных коэффициентов нагрузки

β _m= i₀sinδ/(1-cosφ), где i₀=I₀/I₁ [1]

Для этих трёх значений показаны также кривые 1,2,3 на рис.5. При увеличении cos φ₂=R/(R+X_c)^1/2 максимум смещается вправо (β_m^’ и β_m^”) и при cos φ₂ 1, β_m ∞. Для идеальной емкости:

β _m= i₀sinδ=min (кривая 1, рис. 5).

При увеличении нагрузки угол φ₁ начинает с 0 увеличиваться, cos φ₁ снижаться. Для активной и активно-индуктивных нагрузок cos φ₁ не имеет максимума (кривые 4,5, рис.5). Из векторной диаграммы для таких нагрузок (рис.3) было получено приближенное выражение для cos φ₁

cos φ₁= cos φ₀+β cos φ₂/(1+β)^1/2 [2]

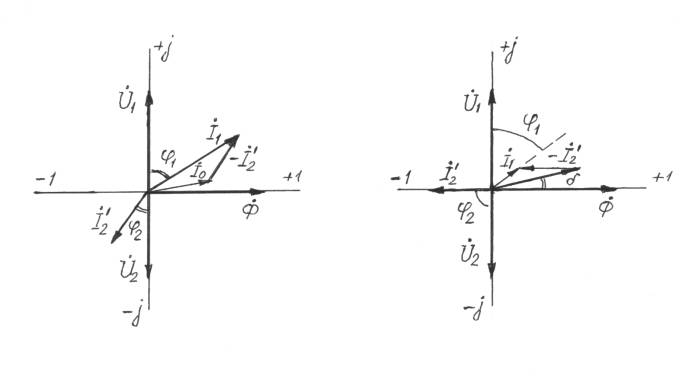
Рис. 3. Векторная диаграмма Рис.4. Векторная диаграмма для

для активно-индуктивной идеальной индуктивной

нагрузки нагрузки.

Для активно-индуктивной нагрузки (диаграмма рис.2) cos φ₀= cos φ₁= cos φ₂=const, т.е. при увеличении β cos φ₁ остаётся неизменным (прямая 6 рис.5). И, наконец для идеальной индуктивной нагрузки (рис.4) cos φ₁ спадает от cos φ₀ до нуля(кривая 7 рис.5).

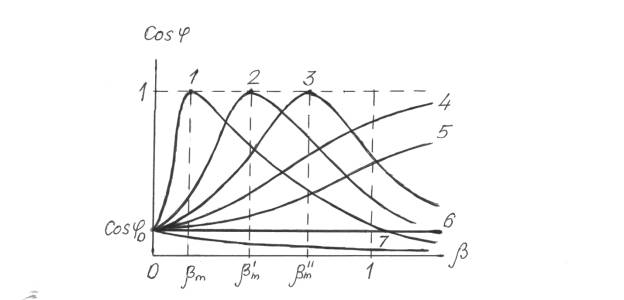
Рис. 5. Зависимость cos φ=f(β).

Построение характеристики коэффициента полезного действия трансформатора η=f(β) (рис.6) производится по известной формуле, включающей в себя величину полной мощности S_н, коэффициент мощности нагрузки cos φ₂, а потери мощности в обмотках Р_к и в магнитопроводе Р_о. Положение максимума кривых не зависит от характера нагрузки и определяется по соотношению β_m=(P₀/P_k)^1/2. После определенного таким образом максимума кривых, КПД при дальнейшем увеличении β начинает уменьшаться. Теоретически эти кривые пересекают ось β в точках короткого замыкания (рис. 6).

Приближенные значения коэффициентов нагрузки β_к, соответствующие режиму короткого замыкания были определены из равенства потерь активной мощности трансформатора

Р₀+β²P_k=S_нβcosφ₂ [3]

Отсюда, пренебрегая потерями холостого хода находим кратность тока короткого замыкания

β_к= cosφ₂ Sн/P_k [4]

Практический расчет КПД для сколь угодно большого значения β дает лишь приближение КПД к нулю. На рис. 6 это показано пунктиром. Зависимости η=f(β) даны для различных значений cosφ₂. Для кривых 1,2 и 3 коэффициенты мощности нагрузки находятся в таком соотношении

cosφ₂⁽¹⁾> cosφ₂⁽²⁾ >cosφ₂⁽³⁾. Соответственно и кратность токов короткого замыкания находится также в соотношении β_к1 >β_к2 >β_к3.

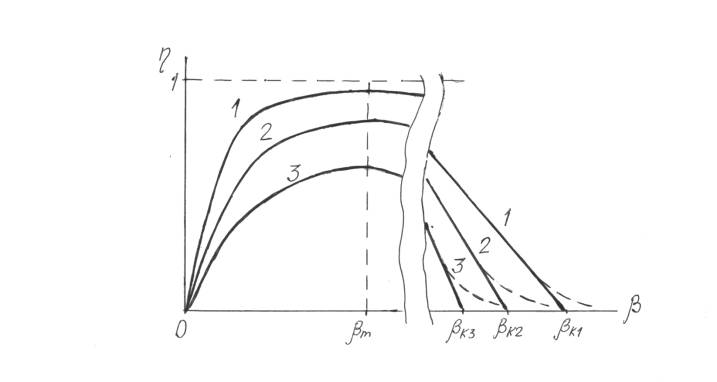
Рис. 6. Зависимость η=f(β).

Сведения об авторах

1. Соборницкий Владимир Иванович – доцент кафедры электротехники Украинского государственного химико-технологического университета, кандидат технических наук. Раб. тел. 753-56-34. Дом. адрес: пр. Кирова, 107а, кв. 97.

2. Павлюс Сергей Григориевич – заведующий кафедрой электротехники Украинского государственного химико-технологичного университета, кандидат технических наук. Раб. тел. 753-56-34. Дом. адрес: ул. Шелгунова 15, кв. 18.

3. Апопий Александр Георгиевич – студент III курса Украинского государственного химико- технологического университета.

4. Соборницка Вера Василиевна – доцент кафедры вагонов и вагонного хозяйства Днепропетровского государственного университета железнодорожного транспорта, кандидат технических наук. Дом. адрес: ул. М.Кюри, д.2, кв.6.