Васильев Иван Анатольевич

Санкт-Петербург, ЦНИИ РТК, нач. лаб., к.т.н.

Управление мобильным роботом с лазерным дальномером

Центральный НИИ робототехники и технической кибернетики, Санкт-Петербург, vas@rtc.ru

Введение

Главная цель работы – движение робота в заданную точку. Для достижения этой цели требуется решить следующие задачи:

1. Локализация робота в некоторой системе координат;

2. Построение бинарных карт рабочей зоны;

3. Построение траекторий для движения робота.

Рассмотрим кратко решения всех трёх задач.

Фото робота приведено на рисунке 1.

Рисунок 1 – Мобильный робот

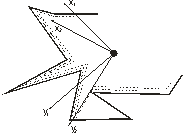
Рисунок 2 – Пример измерения лазерным дальномером

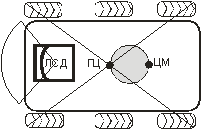
Рисунок 3 – Вид робота сверху.

Сенсорика робота.

В данном случае робот снабжён двумя датчиками: одометрами (датчиками вращения колёс) и лазерным сканирующим дальномером (ЛСД).

Локализация робота.

Без потери общности будем считать, что начало координат совпадает с начальным положением робота. Начальное положение – это то положение робота, которое он имеет при запуске бортового программного обеспечения. Ось абсцисс направлена вправо от продольной оси корпуса, а ось ординат – вперёд, вдоль продольной оси робота.

Пусть робот движется по плоской поверхности, поэтому ось аппликат для наших целей не требуется.

В разных публикациях приведено множество алгоритмов локализации подобного робота, но на практике устойчиво работают лишь самые простые.

Будем называть сканом однократное считывание ЛСД всего ему видимого диапазона. Устойчиво работает локализация, основанная на сравнении двух сканов, измеренных в разное время. Рассмотрим пример двух сканов – см. рисунок 2.

На этом рисунке препятствия показаны сплошной линией, первый скан (с системой координат робота х₁, у₁) – частым пунктиром, второй скан (с системой координат робота х₂, у₂) редким пунктиром. Если попытаться наложить один скан на другой, то довольно просто определить угол, на который повёрнут ЛСД по отношению к предыдущему измерению. Всё это очень просто. На практике же существует следующая проблема. Рассмотрим вид робота сверху на рисунке 3.

На этом рисунке видно, что геометрический центр (ГЦ) робота не совпадает с местом установки дальномера. Это само по себе довольно плохо. Более того, геометрический центр не совпадает и с центром масс (ЦМ) робота! Но и это ещё не всё. Дело в том, что центр поворота робота на месте происходит вокруг случайной оси в каждый момент времени. Это объясняется тем, что подстилающая поверхность, по которой перемещается робот, не идеальная (как и колёса робота). При движении происходит сильное влияние малых неровностей поверхности на перемещение оси поворота.

Экспериментально установлено, что эта ось находится между центром масс и геометрическим центром робота – на рисунке 3 зона нахождения оси показана серым кругом.

Исходя из этого, применение описанного алгоритма «в лоб» приводит к значительным погрешностям, так как ЛСД не поворачивается на месте, а перемещается по некоторой кривой. Следовательно, картина сканов искажается, и прямое их сопоставление приводит к ошибкам.

Для минимизации этого влияния требуется преобразовать сканы из системы координат ЛСД в СК оси поворота. Но, так как ось поворота неизвестна, то видится правильным преобразование в СК ГЦ. Само это преобразование не может вызывать затруднений кроме одной тонкости – рассмотрим рисунок 4.

Рисунок 4 – Схема преобразования координат

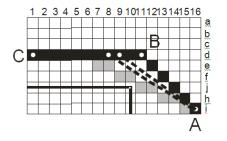
Рисунок 5 – Бинарная карта

Рисунок 6 – построенная траектория.

На этом рисунке жирной ломаной линией показано препятствие. Две системы координат – это система координат ЛСД и система координат, связанная с геометрическим центром робота. На рисунке видно, что, например, отрезки 4-5 и 5-6 видны дальномеру, но не могут быть видны из начала СК ГЦ. Следовательно, при преобразовании координат требуется отбросить все те объекты, которые не видны из начала СК ГЦ. Делается это очень просто. Если последующая точка имеет угол в скане меньше предыдущей (для точек справа от середины), или больше (для точек слева) – то эта точка отбрасывается. На рисунке 4 видно, что отрезок 1-2 мешает увидеть часть отрезка 2-3 из ГЦ. Но, так как этот отрезок вообще не виден из ЛСД, то это не имеет значения.

Здесь надо отметить, что зона преобразованных измерений будет меньше, чем у ЛСД, так как препятствия, находящиеся слева и справа видны под другими углами. На рисунке крайние точки измерений обозначены буквами А и В. Соответственно, диапазон измерений уменьшается до величины угла АО _ГЦ В.

Для упрощения сопоставления далее требуется новый набор измерений привести к равномерной сетке. Для определённости сетку требуется делать с дискретностью такой же, как и у дальномера.

Такой метод был разработан, реализован и отработан автором.

Построение бинарных карт рабочей зоны.

Здесь предполагается, что вначале карта окружающего пространства всегда известна. Во время работы робот уточняет карту, если в реальной ситуации в окружающем пространстве произошли изменения.

Здесь возможны два крайних случая: 1) Карта полностью неизвестна. В этом случае считаем изначальную карту пустой, а во время работы робот добавляет к пустой карте реальные объекты; 2) Карта известна полностью.

Бинарная карта состоит из ячеек, которые могут иметь две характеристики: «занято» или «свободно». Удобство такой карты очевидно: она устойчива к небольшим погрешностям измерений. Также у таких карт есть свойство «толщины» линии. Рассмотрим на рисунке 5 эти утверждения.

На этом рисунке приведена сетка 4х3 – аналог графического отображения сетки бинарной карты. Жирной прямой чертой обозначено препятствие окружающего пространства.

На этом рисунке облако точек, находящееся в ячейке С2, является неточным измерением препятствия. Но такая погрешность не оказывает влияния на бинарную карту, так как карта дискретна. Эффект «толщины» можно продемонстрировать так: для приведённой прямой линии, набор занятых ячеек карты будет не прямой. Гарантированно будут считаться занятыми ячейки, выделенные серым цветом. Более того, по причинам того, что линия препятствия проходит через точку η, и погрешностей измерений, будут считаться занятыми и обе ячейки, обозначенные штриховкой. Всего будут занятыми ячейки А1, А2, В1, В2, С2, D2, D3. А если погрешность такая же, как в ячейке С2, то, вероятно, попадёт в разряд занятых и ячейка С3 (как, возможно, и С1).

По этой причине прямая линия на бинарной карте будет занимать довольно широкую полосу.

Само построение бинарной карты довольно просто. Рассмотрим его подробно. Пусть ЛСД измеряет точку с полярными координатами l и α. Пусть текущее положение робота X, Y, β. Тогда измеренная точка, в СК рабочей зоны робота, будет иметь координаты:

x = X + l cos(α+β)

y = Y + l sin(α+β)

Затем, чтобы получить целочисленные координаты ячейки (i,j) карты, в которой находится текущая точка, требуется выполнить формулы:

i = [x/lx]

j = [y/ly]

где [] – целая часть внутрискобочного выражения;

lx, ly – размеры ячейки карты по абсциссе и по ординате соответственно.

То есть, ячейка карты, в которую в настоящее время обозревает ЛСД имеет номер (i,j). Так как несколько измерений ЛСД могут обозревать одну и ту же ячейку карты, то имеет смысл под ячейкой карты вместо простого бинарного флага понимать счётчик, в котором считается количество измерений объекта, попадающего в данную ячейку. Ячейка будет считаться занятой, если счётчик имеет значение не менее некоторого заданного порога (порог может зависеть от расстояния до дальномера, и, видимо должен определяться экспериментально). Это имеет смысл для того, чтобы отсечь случайные выбросы измерений, случайные погрешности дальномера и случайные ошибочные измерения, включая динамические препятствия.

Для отсечки изменяющихся препятствий, появляющихся и исчезающих, требуется чистка карты. Чистка осуществляется следующим образом: каждый луч дальномера пересекает свободные ячейки карты. Эти ячейки могли ранее быть занятыми, поэтому в пересекаемые ячейки принудительно заносится счётчик 0 (ноль).

И здесь есть тонкость. Дело в том, что луч дальномера пересекает лишь те ячейки карты, которые лежат между ЛСД и препятствием. Если у дальномера было ошибочное измерение дальше, чем препятствие, и случилось так, что это измерение попало в ячейку за препятствием, то эта ячейка не может быть вычищена, пока робот не попадёт в зону за препятствием.

Исходя из вышеперечисленных причин, контуры препятствий на бинарной карте не могут быть тонкими.

Метод бинарных карт был почерпнут из публикации, реализован и отработан автором. Метод хорош и устойчив в том случае, когда число ячеек не очень велико. Реальные карты с числом ячеек порядка сотен тысяч уже работают с некоторыми проблемами в скорости счета. В этом случае не требуется рассматривать на каждом шаге управления всю карту, так как лазерный сканирующий дальномер не может обозревать всю рабочую зону.

Построение траекторий

Постановка задачи построения траекторий следующая: есть бинарная карта, известно положение робота на этой карте. Задаются целевые координаты на этой карте такие, чтобы целевая точка была достижима, т.е., цель не должна быть внутри препятствия и существовал маршрут, соединяющий текущее положение робота с целевым, не пересекающий препятствия и не выходящий за границы карты.

Алгоритмы проезда по бинарной карте известны давно (например, [1]), и подробно обсуждать их здесь нет необходимости. Скажу лишь то, что ячеистая структура карты представляется графом так: ячейки карты – вершины, а переход от ячейки к ячейке – дуги графа. Для нахождения траектории требуется применить любой алгоритм прохода по графу. Для целей построения траекторий чаще всего используют алгоритм Дейкстры или его модификацию, так называемый алгоритм «А-со звёздочкой» (A-star algorithm, А*).

В этих методах есть две сложности. Первая заключается в том, что траектория, полученная методами прохода по графу, требует сглаживания. На рисунке 6 приведена типичная траектория, полученная по алгоритму А* и имеющая стартовую точку А и конечную – С.

На этом рисунке чёрными квадратами обозначена построенная траектория. Пунктирными линиями показано то, как траектория сглаживается. Проводим прямую из начальной ячейки (А) в следующую ячейку и смотрим, нет ли пересечений с препятствиями. Если нет, то берём следующую точку и выполняем эту же процедуру. Этот алгоритм выравнивания довольно быстр и надёжен, но приводит ко второй трудности.

Серыми квадратами закрашены те ячейки, которые претендуют на роль новой (выровненной) траектории, а черной угловой линией обозначено препятствие. На рисунке видно, что угол препятствия, находящийся в точке (j, 10) может мешать проехать роботу, если робот поедет по «серой» траектории. Исходя из этого для движения робота из точки А требуется довернуть робот так, чтобы он двигался не в точку (d,5), куда его приведёт «серая» траектория, а мимо этого угла препятствия, который «виден» дальномеру из точки А. Эта, казалось бы, мелкая поправка сильно оптимизирует время проезда по траектории, так как роботу не потребуется вблизи угла препятствия останавливаться и маневрировать.

Для уверенного движения по траектории робот должен в каждой точке поворота останавливаться и перестаивать траекторию, так как могут открыться новые, ранее неизвестные препятствия а также робот может сбиться с траектории по причине погрешностей отработки движения. Перестройка траектории требуется и еще по причине погрешностей при движении робота.

Заключение.

Все данные методы управления мобильным роботом применяются на вышеописанной платформе. А также были частично применены и на других мобильных роботах, созданных в ЦНИИ РТК.

Простейший метод локализации уверенно работает для любой рабочей зоны, в отличие от сложных методов [2, 3].

Построение бинарных карт позволяет с требуемой точностью отразить рабочую зону, в которой перемещается робот.

Литература

1. И.А.Васильев. Построение траекторий движения для колёсного мобильного робота, снабжённого лазерным сканирующим дальномером. // Труды XXI Международной научно-технической конференции «Экстремальная робототехника» - 2010.

2. Chang Shu, Hillary Buxton. A Parallel Path Algorithm for Mobile Robots. // Travelling Salesman Problem, Book edited by: Federico Greco, ISBN 978-953-7619-10-7, September 2008, I-Tech, Vienna, Austria

3. Зенкевич С. Л., Минин А.А. Построение карты мобильным роботом, оснащенным лазерным дальномером, методом рекуррентной фильтрации. // Мехатроника, автоматизация, управление. 2007. №8.