Лутов В.А.

Санкт-Петербургский государственный университет технологии и дизайна, Россия

ОСОБЕННОСТИ РАСЧЕТА ДВУОСНОГО НАПРЯЖЕННО-ДЕФОРМИРОВАНОГО СОСТОЯНИЯ МЯГКОЙ ЦИЛИНДРИЧЕСКОЙ ТРУБЫ, ТРАНСФОРМИРОВАННОЙ В ПЛОСКОЕ КОЛЬЦО

Задачи определения напряженно-деформированного состояния мягких оболочек при заданных внешних нагрузках возникают при создании упаковок для жидких и сыпучих сред, при формировании разнообразных композитных изделий. Особый интерес для исследователя представляют случаи, допускающие получение аналитических решений и позволяющие решать задачи оптимизации параметров оболочки при проектировании включающих ее конструкций.

Рассмотрим осесимметричную деформацию растяжимой трубы, кромки которой закреплены на окружностях. Будем считать, что в недеформированном состоянии труба имеет радиус , ее кромки перпендикулярны к ее оси, а структура трубы соответствует текстильному переплетению полотняного типа, при котором одно семейство нитей идет вдоль направляющих трубы, а другое - вдоль образующих.

Используя в качестве лагранжевых координат частиц оболочки цилиндрические координаты и предполагая, что оболочка в исходном и в деформированном состояниях симметрична относительно оси , совмещенной с осью цилиндрической координатной системы , представим радиус-вектор частицы недеформированной и деформированной оболочки в виде

(1)

соответственно.

Будем использовать следующие обозначения:

(2)

Метрические коэффициенты недеформированной и деформированной оболочки, соответственно, равны

(3)

и

(4)

а величины напряжений определяются равенствами [1,2]

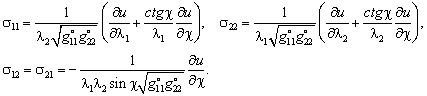(5)

Здесь - кратности удлинений линий лагранжевых координат, - величина угла между координатными линиями, - плотность потенциальной энергии деформации оболочки.

Запишем плотность потенциальной энергии деформации в виде

(6)

где - параметр, характеризующий упругость нитей, образующих оболочку.

Используя равенства (3), (4), (6) запишем выражения (5) величин напряжений в виде

(7)

При отсутствии внешней распределенной нагрузки уравнения равновесия оболочки могут быть записаны в виде [1, 2]

(8)

где

(9)

На основе (9), пользуясь независимостью скалярных характеристик состояния оболочки от угла , первое из уравнений (8) запишем в виде

(10)

Предположим, что кромки трубы, имеющей в недеформированном состоянии длину , растянуты и перемещены так, что труба превратилась в плоское кольцо с внутренним и внешним радиусами, равными и , соответственно.

Считая, что это кольцо находится в плоскости , перепишем уравнение (10) в виде

(11)

В силу линейной независимости синуса и косинуса, а также независимости скалярных характеристик состояния оболочки от угла , уравнение (11) эквивалентно скалярному уравнению

(12)

Легко видеть [3], что задача сводится к интегрированию уравнения

(13)

решение которого при граничных условиях имеет вид

(14)

Вычисляя напряжения на основе формул (7) с учетом (3) и (4), будем иметь

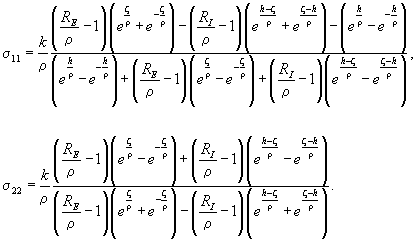(15)

Равенства (14) и (15) при определенных значениях входящих в них параметров описывают двуосное напряженно-деформированное состояние части трубы, трансформировавшейся в плоское кольцо.

На рис. 1 и 2 показаны графики зависимостей координаты частицы оболочки от ее лагранжевой координаты и напряжений и от , характеризующих напряженно-деформированное состояние плоского кольца для следующих значений параметров задачи:

Рисунок 1 - График зависимости отношения

от лагранжевой координаты частицы оболочки

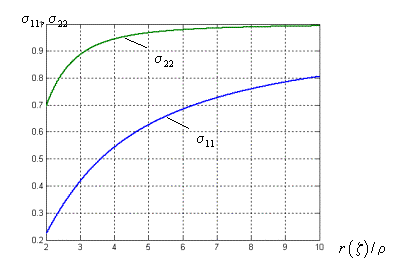
Рисунок 2 - Графики зависимостей напряжений и от

Отметим, что при наличии зон складкообразования применение полученных выше уравнений равновесия и выражений для напряжений, плотности потенциальной энергии деформации, кратностей удлинений и относительных удлинений некорректно, что ведет к необходимости проведения дополнительного исследования.

Литература:

1. Полякова Е. В. Прикладные задачи механики мягких оболочек и тканей. Монография / Е.В. Полякова, В.А. Чайкин. – СПб.: СПГУТД, 2006. – 193 с.

2. Чайкин В.А. Прикладные проблемы теории мягких оболочек. Монография / В.А. Чайкин, Е.В. Полякова, П.А. Дятлова. – Спб.: СПГУТД, 2009. – 167 c.

3. Лутов В. А. Осесимметричная задача о деформировании ортотропной мягкой трубы усилиями, приложенными к её кромкам. / В. А. Лутов, В. А. Чайкин, А. Ю. Баранов, Е. В. Полякова. // Дизайн. Материалы. Технология. – 2010. – №3(14) – С. 80–84.

Работа выполнена при поддержке Минобрнауки России (проекты № 2.1.2/3270 и № 2.1.2/13091 в рамках АВЦП «Развитие научного потенциала высшей школы (2009-2011 годы)»).