Технические науки/5. Энергетика

Севостьянов А.В., д.т.н. Дождиков В.И.

Липецкий государственный технический университет, Россия

ЭНЕРГЕТИЧЕСКАЯ ЭФФЕКТИВНОСТЬ ДИСПЕРГИРОВАНИЯ ЖИДКОСТНЫХ СТРУЙ

Для проектирования систем охлаждения и анализа их режимов работы необходимо изучение процесса диспергирования жидкости, истекающей из разбрызгивающего устройства. Основной целью диспергирования жидкости форсунками является получение дисперсного потока капель жидкости, обладающих требуемыми размерами и скоростями на определённом расстоянии от форсунки.

Уравнение баланса энергии жидкости, покидающей форсунку, может иметь вид:

, (1)

где - полная энергия жидкости, - кинетическая энергия капель; - энергия поверхностного натяжения капель, - гидравлические потери энергии;

(2)

- энергия растворённого газа в предположении, что жидкость предельно насыщена газом при давлении ; - атмосферное давление; - коэффициент растворимости газа; - плотность газа; - газовая постоянная; - температура газа, - постоянная адиабаты газа, - давление жидкости перед форсункой, - плотность жидкости, - скорость капли, - диаметр капли, - коэффициент поверхностного натяжения, - скорость потока жидкости на срезе сопла форсунки, - коэффициент сопротивления форсунки. Полагаем, что на выходе из форсунки скорости капель и потока жидкости равны.

Развёрнутая запись уравнения баланса энергии будет иметь вид:

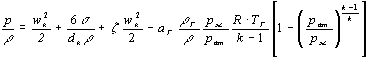, (3)

что приводит к выражению

, (4)

где - коэффициент кинетической энергии, - коэффициент диспергирования, - коэффициент гидравлических потерь,

(4)

- коэффициент энергии растворённого газа.

Оценки показывают, что в уравнении (4) коэффициент имеет значение не менее 0,92, слабо зависит от размера капли в области значения диаметров менее 150 мкм и практически не зависит от размеров для более крупных капель.

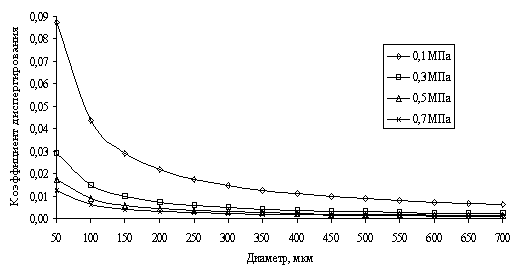
Рис. 1. Связь коэффициента диспергирования с диаметром капли при различных давлениях жидкости

Из приведённых выражений видно, что только коэффициент диспергирования прямо зависит от размера капли, что хорошо видно на рис. 1. Доля энергии, идущая на диспергирование, уменьшается с увеличением диаметра капли и давления жидкости.

Из уравнения (5) следует >1, что в соответствии с выражением (4) приводит к увеличению эффективности диспергирования для всех типов жидкостных форсунок, что хорошо видно на рис. 2. Растворённый газ на малых давлениях примерно вдвое увеличивает коэффициент диспергирования. На более высоких давлениях растворённый газ практически стабилизирует коэффициент диспергирования, увеличивая его примерно в восемь раз.

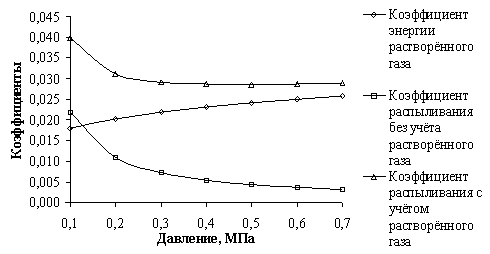
Рис. 2. Влияние растворённого газа на процесс диспергирования для различных давлений жидкости при фиксированном диаметре капли 200 мкм.

Следует отметить, что соотношения (2) и (5) приведены для случая предельного насыщения жидкости газом при давлении p. Такое насыщение происходит в течение длительного времени, что не реализуется в системах охлаждения. Реальные значения коэффициента в действующих системах охлаждения ожидаются меньшими и должны быть определены экспериментально для конкретной охлаждающей установки.

Сразу после выхода из форсунки капли жидкости испытывают ещё и аэродинамическое сопротивление газа, что можно учесть введением в уравнение (4) коэффициента аэродинамических потерь

(6)

Коэффициенты и зависят только от условий выхода жидкости из форсунки и далее остаются постоянными. Отсюда следует, что коэффициент кинетической энергии является функцией расстояния от форсунки. Для анализа зависимости проанализируем движение капли в газожидкостном потоке. С этой целью принят ряд следующих допущений.

Из рассмотрения полностью исключена стадия плёночного течения, что возможно для описания процесса объемного распыливания для некоторых типов форсунок.

Истекающая струя представляет собой расширяющийся эллиптический конус с площадью сечения

, (7)

где и - углы раскрытия эллиптического конуса по осям эллипса

Движение газа в такой струе определяется движением капель. Кроме того, полагается, что массовый расход жидкостной компоненты струи постоянен, а сама жидкостная компонента потока состоит только из монодисперсных сферических капель, и при движении каждой капли учитывается только аэродинамическое сопротивление.

Из выражения (6) видно, что при заданном давлении для каждого сечения струи можно составить баланс энергии

, (8)

где - полная энергия струи, - энергия газовой компоненты струи, или в развёрнутом виде

, (9)

- масса капель; - масса газа; - скорость газа. Отсюда следует выражение для скорости газовой компоненты струи:

, (10)

где - площадь соплового отверстия форсунки.

Как уже упоминалось, на каплю в струе действуют сила инерции и сила аэродинамического давления:

, (11)

где - лобовая площадь капли; С – коэффициент аэродинамического сопротивления [1]:

. (12)

Число Рейнольдса определяется по скорости скольжения

, (13)

где - коэффициент динамической вязкости газа.

Совместное решение уравнений (10) и (11) позволяет найти связь между давлением, диаметром и скоростями газовой и жидкостной компонентами. За основу взяты параметры зон вторичного охлаждения установок непрерывного литья заготовок и данные по форсункам серии «К», которые были разработаны в Липецком госуниверситете.

Сравнение данных по скоростям газовой и жидкостной компонент показывает, что скорость газовой компоненты находится в обратной зависимости от диаметра капли по сравнению со скоростью капли.

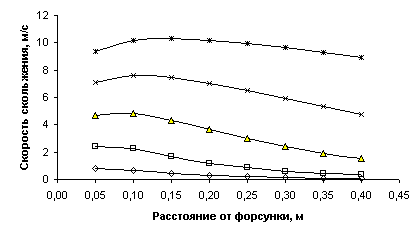
Распределение скорости скольжения для капель различных диаметров (см. рис. 3) явно демонстрирует, что капли малых диаметров имеют скорость скольжения близкую к нулю, т.е. газокапельный поток с каплями диаметром 20 мкм и менее можно считать гомогенным. Поток с каплями диаметром 80 мкм и более на расстоянии 0,4 м всё ещё остаётся гетерогенным с заметной скоростью скольжения.

Рис.3. Распределение скорости скольжения для капель различных диаметров при давлении жидкости 0,5 МПа.

1 – 320 мкм, 2 – 160 мкм, 3 – 80 мкм, 4 – 40 мкм, 5 – 20 мкм.

При эксплуатации систем охлаждения в металлургии очень часто используется вода оборотного цикла с переменной температурой. Представляет некоторый интерес влияние температуры используемой воды на диспергирование жидкости в форсуночных устройствах систем охлаждения.

По соотношению (3) видно, что изменение температуры может повлиять на значения энергетических коэффициентов через плотность жидкости и коэффициент поверхностного натяжения. Плотность воды в диапазоне температур от 0 до 60 °С изменяется на 1,7% [2], что не может заметно повлиять на процесс диспергирования.

Коэффициент поверхностного натяжения на границе вода – воздух в отмеченном диапазоне температур изменяется на 12,5% [2], что должно повлиять на диспергирование. На рис. 4 приведены зависимости коэффициента диспергирования от температуры в диапазоне от 0 до 60 °С для различных размеров капель при давлении воды 0,3 МПа. Хорошо видно, что для капель малых размеров значение коэффициента распыливания заметно падает с ростом температуры. Это означает, что в общем балансе энергии жидкости, покидающей форсунку, доля энергии, приходящаяся на диспергирование, уменьшается. Для капель более крупных размеров этот эффект менее заметен, так для капель средним диаметром 500 мкм это изменение в отмеченном диапазоне температур составляет 5∙10^-6 град^-1 по сравнению с каплями диаметром 100 мкм, для которых это изменение составляет 2,5∙10^-5 град^-1, т.е. в пять раз меньше.

Рис. 4. Влияние температуры воды на коэффициент диспергирования.

На рис. 5 показаны графические зависимости коэффициента энергии растворенного воздуха от температуры воды для различных давлений воды на форсунке. В приведённом диапазоне температур коэффициент энергии растворенного воздуха уменьшается практически вдвое для всех указанных перепадов давления.

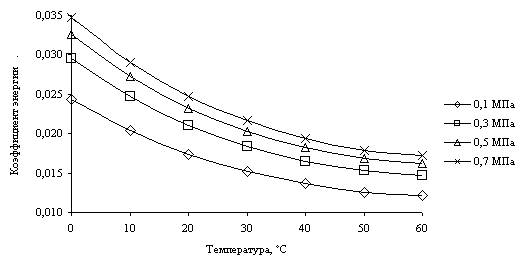
Рис. 5. Влияние температуры на коэффициент энергии растворённого воздуха.

Так как энергия растворённого в воде воздуха способствует диспергированию, то следует ожидать заметного изменения эффективного диспергирования с ростом температуры воды. На рис. 6 приведены соответствующие зависимости для различных размеров капель при перепаде давления на форсунке 0,3 МПа. Рост температуры воды явно понижает эффективное диспергирование для капель всех размеров.

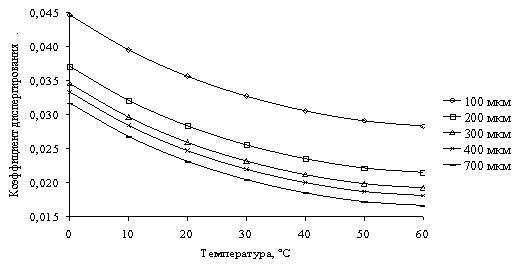
Рис. 6. Влияние температуры на коэффициент диспергирования с учётом растворённого в воде воздуха для различных размеров капель.

Анализ влияния температуры на эффективность диспергирования воды различной температуры в установках охлаждения показывает, что прямое влияние на механическое распыливание невелико и растёт с уменьшением характерного размера капель. Учёт растворённого в воде воздуха показывает более заметное влияние температуры на эффективность диспергирования.

Полученные результаты позволяют оценить влияние основных технологических параметров систем охлаждения на параметры струй, играющих определяющую роль в процессе теплообмена этих струй с высоконагретой твёрдой поверхностью.

Литература:

1. Муштаев В.И., Ульянов В.М. Сушка дисперсных материалов. М.: Химия, 1988. 352 с.

2. Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей. – М.: Физ. мат. лит., 1963. 708 с.