Кишкин А.А., Черненко Д.В., Делков А.В.

Сибирский государственный аэрокосмический университет имени академика М. Ф. Решетнева, г. Красноярск, Россия

Расчет цикла работы паротурбинной установки на низкокипящем рабочем теле

Развитие и модернизация системы электроснабжения предопределяет необходимость использования паротурбинных установок (ПТУ) на низкокипящих рабочих телах (НРТ) для утилизации низкопотенциального и сбросного тепла. С помощью подобных установок можно использовать тепловые сбросы промышленных предприятий, тепло термальных вод и другие источники низкопотенциальной энергии для генерации электроэнергии. В качестве рабочего тела ПТУ НРТ возможно применение хладагентов R22, R134а (температуры кипения в рабочем цикле +60..+80 °С) и R245 для более высоких температур. [1]

В связи с актуальностью использования ПТУ НРТ возрастает потребность анализа, расчета и проектирования подобных установок, что обуславливает потребность в моделировании рабочих циклов установки для описания и оптимизации ее процессов [2].

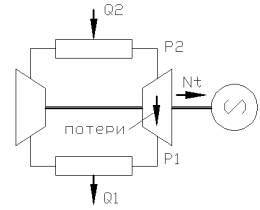
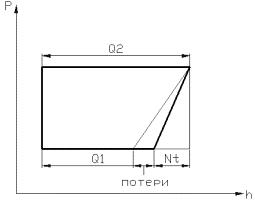
Рис. 1. Схема установки и ее рабочий цикл

В составе ПТУ НРТ (рис. 1) можно выделить две подсистемы – тепловую (испаритель, турбина, конденсатор, питательный насос) и силовую – энергогенерирующую (турбина и генератор). В тепловой подсистеме системе циркулирует НРТ, испаряясь при низких для силовой энергетики температурах (+60 .. +80 °С), срабатываясь на турбине и конденсируясь. В силовой подсистеме снятая с турбины техническая работа идет на генерацию электроэнергии. Процессы в подсистемах взаимосвязаны уравнениями энергетического и материального баланса.

Для описания рабочих процессов в элементах установки и их взаимосвязей можно составить систему уравнений математической модели. Формально система уравнений делится на две части – внутреннюю, описывающую процессы в системе ПТУ, и внешнюю, характеризующую окружающую среду. Внутренняя подсистема, базируясь на уравнениях отдельных элементов, связанных уравнениями балансов системы, дополняется внешними условиями – характеристиками источника и холодильника. Целевая функция модели - параметры работы установки.

Баланс энергий системы ПТУ НРТ в модели представлен следующим образом. На турбине вырабатывается адиабатическая мощность N_ад, зависящая от параметров рабочего тела на входе и на выходе и от массового расхода.

,

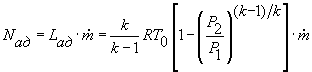где- адиабатная работа газа; - расход газа в турбине; к – показатель адиабаты; - давление газа на входе в турбину; - давление газа на выходе из турбины.

Адиабатическая мощность расходуется на техническую мощность генератора Nt и потери в самой турбине N_потерь.

Баланс мощностей можно проследить по рабочему циклу (рис. 1)

где - тепловой поток на конденсаторе; - тепловой поток на испарителе.

Материальный баланс заключается в одинаковом массовом расходе в элементах системы. Составные части баланса – расходы через насос и турбину.

На основе вышеприведенных уравнений математической модели ПТУ НРТ был составлен алгоритм расчета и проведены численные исследования рабочих режимов установки и энергетического баланса турбины. Варьируемый параметр – напор насоса, который задает перепад давлений между теплообменниками. При этом в системе меняются два параметра – удельная работа и массовый расход.

Алгоритм расчета характеризуется следующими параметрами. Исходные данные: температура нагревателя, температура холодильника, геометрия рабочих элементов (профиль соплового аппарата, площадь теплообмена испарителя и конденсатора, диаметр колеса турбины, характерные углы наклона сопел, входа и выхода лопатки). Рассчитываемые параметры: массовый расход рабочего тела, адиабатная мощность турбины, потери в турбине, термодинамические параметры рабочего тела на входе и на выходе из турбины, скорости рабочего тела в проточной части турбины, потребная мощность насоса, КПД турбины.

Решение ведется следующим способом: по исходным данным определяются основные термодинамические параметры рабочего цикла – давления и расходы, температуры кипения и конденсации. Далее определяются параметры работы турбины. По вычисленным давлению и удельному объему на входе в сопловой аппарат определяется адиабатическая работа газа и потери в сопле. Далее для потоков пара в каналах рабочего колеса строятся треугольники скоростей, определяется скорость на выходе из рабочей решетки, потери в колесе и с выходной скоростью. Далее вычисляется угловая скорость, механические и вентиляционные потери. Для вычислений параметры рабочего тела берутся из базы данных свойств, формально представляющей собой математическую поверхность.

Математическая поверхность состояния (рис. 2) низкокипящего рабочего тела в координатах давления P, удельного объема V и температуры T позволяет проводить расчеты циклов энергоустановок численными методами с учетом непрерывного изменения свойств. Кроме того, с использованием поверхности возможно получение основных параметров тела (энтальпия, энтропия, теплоемкость, скорость звука и т.д.) с использованием дифференциальных уравнений термодинамики. Представленная поверхность построена по таблицам состояния фреона.

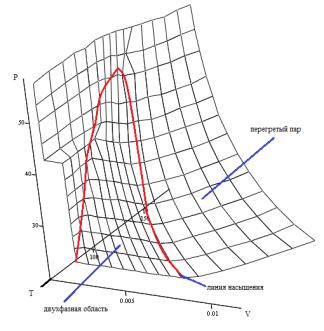
Рис. 2. Поверхность состояния фреона R22

Результаты расчета баланса турбины по модели приведены на рис. 3. Установлена тенденция увеличения КПД с наращиванием адиабатной мощности турбины. Это связано с перестройкой треугольников скоростей и уменьшением потерь с выходной скоростью. Оптимальными по КПД получаются решения с большими напорами насоса.

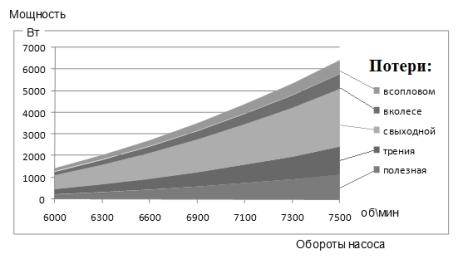
Рис. 3. Баланс мощностей турбины

Планируется доработка математической модели паротурбинной установки. Корректировке подвергнутся расчетные коэффициенты потерь, которые определяются при анализе экспериментальных данных. В результате на основе полученной модели предполагается проводить оптимизацию паротурбиной установки на низкокипящем рабочем теле.

Работа выполнена при финансовой поддержке КГАУ «Красноярский краевой фонд поддержки научной и научно-технической деятельности».

Литература:

1. Brasz Joost J. Power Production from a Moderate -Temperature Geothermal Resource // Joost J. Brasz, Bruce P. Biederman, Gwen Holdmann. Paper presented at the Geothermal Resources Council Annual Meeting September 25-28th, 2005; Reno, NV, USA.

2. Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. М.: Физматлит, 2001.