Московский государственный открытый университет, Россия

Желонкин А.И., д.т.н.

Динамические процессы молекулярноэлектронного

преобразователя потока электролита

 

Физические процессы в молекулярноэлектронных преобразователях потока электролита в электрический сигнал определяются электрохимическими (окислительно-восстановительными) реакциями и гидродинамическими процессами, определяющими тепломассообмен в движущей среде. При определении параметров процесса следует учитывать форму, размер и температуру обтекаемой поверхности рабочего канала, скорость, температуру и физические свойства движущей среды (электролита). Для решения проблемы необходимо установить функциональные зависимости между физическими переменными, которые могут изменяться во времени и пространстве. При этом рассмотрим лишь ламинарный поток электролита, когда имеется закономерная зависимость величины выходного тока от конвективной доставки электроактивныцх ионов к поверхности электродов. Основными параметрами электролита, определяющими динамические процессы, являются коэффициент диффузии и вязкость.

Характеристики диффузионного потока (перенос ионов к поверхности рабочего электрода) при наличии движения раствора электролита определяются при рассмотрении процессов тепломассообмена и собственно диффузии. Процессы переноса импульса, тепла и массы в потоке жидкости описываются в общем виде с помощью следующей системы уравнений:

 Уравнение неразрывности:

 

                                                             (1)

 

где mp – изменение массы, обусловленное диссипацией энергии, которое пренебрежимо мало в большинстве гидродинамических задач.

 Уравнение движения вязкой жидкости (уравнение Навье – Стокса):

  (2)

где:субстанциональная производная;

U – физическая величина; V – скорость потока величины;

W – плотность потока;

 Fx , F y, Fz  – проекции вектора массовых сил на оси координат;

 p – давление в рассматриваемой точке;

 m – динамический коэффициент вязкости.

Уравнение энергии:

                                                    (3)

Левая часть уравнения (3) определяет скорость изменения полной энергии Е в единице объема движущей среды. Правая часть характеризует работу, совершаемую давлением среды – р, энергию, передаваемую теплопроводностью – Ql , перенос тепла излучением – Qh , количество тепла, выделенное внутренними источниками – Qо , энергию естественной – Qg и вынужденной конвекции – Qv и диссипацию энергии U, V, W  напряжений по координатам x, y, z – mФ.

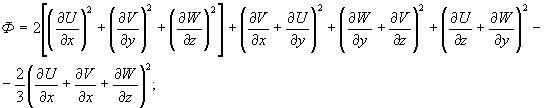      (4)

  Рассматривая изотермический процесс в электрохимической ячейке, получим систему уравнений, описывающих двумерное стационарное течение:

  Уравнение неразрывности:        ;                                       (5)

  Уравнение движения для скорости Vх:

                          ;                      (6)            

для установившегося движения  жидкости и при     , что выполняется в конструкциях, получим уравнение гидродинамического слоя:

                                            ;                                        (7)                                

где r – плотность рабочей жидкости, h – кинематическая вязкость.

 Уравнение конвективной диффузии представляет собой линейное уравнение в частных производных с переменными коэффициентами [2]:

                             ;                       

 Вблизи электрода возникает диффузионный слой (аналогичный гидродинамическому пограничному слою Прандтля), где основополагающим становится конвективный поток, а концентрации С выравниваются от приэлектродного значения (практически от 0)  до исходного значения С0 в объеме раствора. В этом же слое происходит ионное перераспределение электрического тока. Для стационарного случая двухкоординатной системы уравнение пограничного диффузионного слоя имеет вид:

                                           ;                                          (8)       

 Таким образом, описание гидродинамики и диффузии в канале диффузионного преобразователя  предполагает совместное решение уравнений Навье - Стокса (7) и конвективной диффузии (8). Экспериментальные и теоретические исследования [2] показали, что решение системы уравнений может быть с достаточной степенью точности заменено независимым решением уравнения гидродинамики и использованием полученного результата для решения уравнения конвективной диффузии. Для стабилизированного движения электролита средняя скорость определится как: 

                                                

где: l – длина канала, Sk – сечение канала, Rг – гидросопротивление канала.

Откуда:    – для прямоугольного (шириной h) и цилиндрического (радиусом r) каналов, соответственно.

Плотность тока, характеризуемая скоростью диффузии электроактивных ионов электролита к считывающему электроду и полный ток определяются следующими выражениями:; ; где:  F – число Фарадея,  S – площадь поверхности считывающего электрода, - нормаль к фронтальной поверхности, определяющей движение электролита.

Решение системы уравнений может быть, с достаточной степенью точности, заменено независимым решением одного из уравнений и использованием полученного результата для решения системы [2].

При начальных и граничных условиях: C(0,t)=0;  C(X,0)=C0;  0 < X £ l; распределение безразмерной концентрации () для цилиндрического канала определяется выражением:

                               

Среднее значение концентрации в элементарном объеме:

              

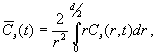
где: r – текущий радиус элементарного объема, I0, I1 – функции Бесселя первого рода нулевого порядка, ln – корни функции Бесселя,     bn= 4 / ln ; F0 = 4Dt/d2 .

Изменение средней концентрации в потоке электролита определяется как:

                           

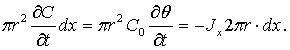
Поток массы электролита на стенках цилиндрического канала будет равен:

                      

Учитывая, что t = x/V  и интегрируя по активной поверхности электрода, получим зависимость величины тока преобразователя от гидродинамического потока электролита:

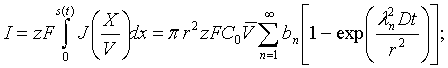                      (9)

и от перепада давления:

 

                    ,      z  – зарядность ионов.   (10)                                   

Различные схемы включения и расположения электродов можно охарактеризовать соответствующими граничными условиями:

 

       1. C(0,Y) = 0;   

           C(h,Y) = 0;         – трех или четырех электродная система с внутренним

                                                  C(X,0) = 0;           катодом.

 

           2. С(0,Y) =  0;

                       C(X,Y)              

               X        = 0        – то же с внешними катодами.

           C(X,0) = C0;

       

      

       3. С(0,Y) =0;

           C(h,Y) = C0;        – двух электродная система.

           C(X,0) = 0;

 

Решение уравнения диффузии при заданных граничных условиях дает следующие значения для выходного тока:

                

               

               

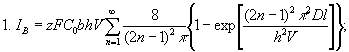
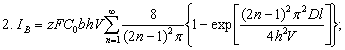
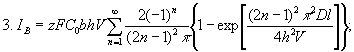
Выражение для тока представляет сумму бесконечного числа экспонент, затухающих с постоянной времени T = h2/ln2D. Величина времени затухания уменьшается  в  каждом последующем  слагаемом   (при n=1, T = r2/ 5,75D; n=2,

T = r2/ 31D; n = 3, T = r2/ 75D и т.д.), в практических расчетах ограничиваются первым слагаемым. Ток определяется следующими выражениями:

                       I = 2,2 r2zFCoV[ 1- exp(-5,75Dt/ r2)];                                  (11)

                                                       (12)                              

Передаточные функции диффузионного преобразователя  будут иметь вид:

 Wд1 (p) =; Wд2(p) =  ;  (p) =      (13)

где: K1= 0,0172 C0 zFd4 / mL; Kд = 0,55C0 zFd2; Tд = d2 /23D; d=2r.                (14)

       X – смещение электролита.

   Для преобразователя с переменной площадью электродов получим [2]:

             W '(p) =     K'д = 2,2 C0 zFDdэ /d;                               (15)                                                     

где  dэ – диаметр электрода; d – толщина двойного слоя.

Для канала в виде плоской щели с высотой h и шириной b получим [2]:

            K1 = 0,076 C0 zFbh3 / mL; Kд = 0,92C0 zFbh; Tд = h2 / 9,2D.           (16)

Коэффициенты для пористого канала определяются по формулам:

            K1 = C0 zFkS/mL;  Kд = 0,55C0 zFnd2эф = 0,55C0 zFd20P2 / m2n;     (17)

           Tд = d2эфn/23D = d20 P2 / 23D m2n = 1,39 km / D;                           

где: K – проницаемость канала; d0  – средний диаметр пор; n – число пор;

 P = V0/Vп-  пористость; V0 – объем пор; Vп – объем пористого канала;

  m – геометрический параметр пор; dэф =  – эффективный диаметр пор.

   Чувствительность преобразователей с элементарными каналами (14), (15), (16), (17) зависит от  характерного размера канала h(d), однако с его увеличением сужается частотный диапазон. Уменьшить характерный размер, не увеличивая гидравлическое сопротивление, т.е. расширить диапазон, не уменьшая чувствительность, удается плоско-радиальной конструкцией измерительного канала [2]. В (15) подставляем следующее значение средней скорости электролита для такого канала: 

                                            ;

где: d>>l; d1, l – диаметр входного отверстия канала и его длина, d2 – диаметр плоско-радиального канала.

В этом случае коэффициенты преобразования равны:

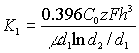                     ;Kд = 2,89C0 zFhd2 lnd2/d1;                         

чувствительность увеличивается более чем в пять раз.

 

                                              Литература

1. Желонкин А.И. Математическое моделирование  диффузионного преобразователя. Материали   за v11 Международна  научна практична конференция«Найновите постижения  на европейската наука - 2011», том 42. С.44-46. Технологии. София «Бял град-бг» оод 2011.

2. Лидоренко Н.С. и др. Введение в молекулярную электронику. – М.: Энергоатомиздат, 1985. – 165 с.

3. Желонкин А.И. Молекулярно-электронные аналоговые преобразователи неэлектрических сигналов. Структурное и математическое моделирование, конструкторско-технологический синтез. – М.: Квадрат-С, 2004. – 140 с.