Технические науки /6. Электротехника и радиоэлектроника

К.т.н. Рапин В.В.

Украинская инженерно –педагогическая академия

Автогенераторная следящая система

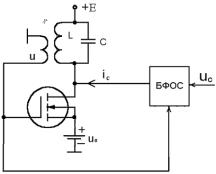
Способность автогенератора работать в режиме, когда внешний сигнал навязывает частоту колебаний, в некотором достаточно широком диапазоне, позволяет использовать его в качестве основного элемента следящей системы. Если этот сигнал полигармонический, то синхронизация осуществляется на первой гармонике, а уровень высших гармоник сигнала синхронизированного автогенератора в этом случае существенно меньше уровня высших гармоник сигнала синхронизации, что допускает применение его в качестве следящего фильтра. Преимущество такой следящей системы состоит в том, что захват производится автоматически в широком диапазоне частот, как и отслеживание. Структурная схема автогенераторной следящей системы показана на рис 1.

Рис. 1. Структурная схема следящей системы с двукратной нелинейной

обратной связью: 1 – широкополосный фильтр; 2, 3 – блоки формирования нелинейной обратной связи; 4 – блок стабилизации амплитуды сигнала; 5 – преобразователь напряжения в ток; 6 – автогенератор.

Структурная схема блока формирования нелинейной обратной связи представлена на рис. 2.

Рис. 2. Блок формирования нелинейной обратной связи: 1, 3, 5 – широкополосные фильтры; 2 – схема возведения в квадрат; 4 – перемножитель.

Исходя из практического использования, ограничимся только учетом первой и второй гармонических составляющих. В этом случае граничные частоты фильтров 1 и 5 устанавливаются равными граничным частотам следящего фильтра. Верхняя граничная частота фильтра 2 равняется удвоенной верхней граничной частоте следящего фильтра, а нижняя граничная частота совпадает с нижней граничной частотой следящего фильтра.

Следящий фильтр может работать в двух режимах. Первый это когда частота первой гармоники сигнала синхронизации и автогенератора, принимает такие значения, при которых через входной широкополосный фильтр 1 (рис. 1) а также через фильтры 1 и 5 (рис.2) проходят только первые гармоники сигналов. Второй режим наступает тогда, когда в полосы пропускания вышеуказанных фильтров с фиксированной полосой пропускания попадают первая и вторая гармоники сигналов внешнего и автогенератора.

Рассмотрим первый режим. Допустим, что внешний полигармонический сигнал после прохождения входного фильтра 1 (рис. 1) описывается выражением , а полигармонический сигнал обратной связи после прохождения фильтра 1 (рис. 2) имеет вид , где фазовый сдвиг, вносимый фильтром 1. Затем, в соответствии с алгоритмом формирования нелинейной обратной связи, возводим сигнал обратной связи в квадрат, устраняем постоянную составляющую, а переменную перемножаем с сигналом синхронизации. Третья гармоника устраняется фильтром 5, а первая, и есть непосредственный сигнал синхронизации , где , . Для данного режима работы непосредственный сигнал синхронизации не содержит второй гармоники. Вторая гармоническая составляющая сигнала автогенератора будет определяться только самим автогенератором.

Во втором блоке формирования нелинейной обратной связи процедура повторяется. В результате имеем . Полученная амплитуда особой роли не играет, поскольку она устанавливается исходя из требуемой полосы синхронизации. Затем, после стабилизации амплитуды и преобразования в ток, этот сигнал поступает в контур автогенератора для синхронизации его колебаний. И в этом случае непосредственный сигнал синхронизации не содержит второй гармоники, а вторая гармоническая составляющая сигнала автогенератора будет определяться только самим автогенератором.

Рассмотрим теперь второй режим работы следящего фильтра. Допустим, что внешний сигнал синхронизации после прохождения входного фильтра 1 (рис. 1) описывается выражением , а полигармонический сигнал обратной связи после прохождения фильтра 1 (рис. 2) записывается в виде , где и фазовые сдвиги, вносимые фильтром 1. После преобразования в блоках формирования нелинейной обратной связи, стабилизации амплитуды и преобразования в ток имеем , .

Принципиальная схема автогенератора следящей системы показана на рис 3.

Рис.3 Схема следящего фильтра

Основное уравнение автогенератора имеет вид где . Используя метод разделения частот получаем укороченную комплексную модель

(1)

Вводим безразмерную амплитуду первой гармонической составляющей сигнала автогенератора , где , - амплитуды сигналов синхронизированного автогенератора и автономного. Тогда укороченные уравнения для первой гармонической составляющей сигнала автогенератора имеют вид

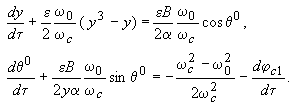
где , , , , -амплитуды первых гармоник непосредственного сигнала синхронизации и импульса тока усилительного элемента автогенератора в автономном режиме. Решение этой системы позволяет определить величину амплитуды и сдвига фазы первой гармонической составляющей сигнала синхронизированного автогенератора. Второе уравнение системы (1) дает относительную величину второй гармоники сигнала автогенератора. ^{Для первого режима работы фильтра, когда .}

_.

_{Во втором режиме работы . В результате имеем}

_.

_{Проведенные исследования и полученные соотношения позволяют разрабатывать автогенераторные следящие системы различного назначения с коэффициентами перекрытия полосы захвата до величин порядка 2.5.}

_{Литература}

1. Карпенко А.Ф., Рапин В.В. Автогенераторные следящие фильтры с фазовой обратной связью в системах измерения частоты вращения ротора турбины.. В сб. научных трудов пятого международного конгресса двигателестрои-телей. Харьков: Выпуск 19, 2000. C. 466-467.

2. Патент № 46173. Украина МПК(2009) H04L25/14. Автогенераторний слідкувальний фільтр з подвійним зворотнім зв’язком / Рапін В.В. -2009. Бюл. № 23.

3. Рапин В.В., Хуторненко С.В. Розробка математичної моделі автогенераторного відслідковуючого фільтру // Системи обробки інформації. Збірник наукових праць. -2005. -Випуск 1. -С. 75- 80