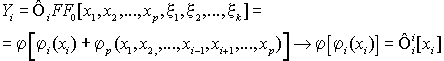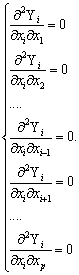Технические науки/6. Электротехника и радиоэлектроника

К.т.н. Воробей Р.И., д.т.н. Гусев О.К., д.т.н. Жарин А.Л., к.т.н. Свистун А.И., к.т.н. Тявловский А.К., к.ф.-м.н. Тявловский К.Л.

Белорусский национальный технический университет, Беларусь

Применение методологии многопараметрических измерений параметров объектов к разработке метода зондовой электрометрии на основе невибрирующего зонда Кельвина

Применяемый в зондовой электрометрии метод Кельвина-Зисмана [1], основанный на использовании вибрирующего конденсатора (зонда Кельвина), наряду с известными преимуществами (бесконтактностью, высокой чувствительностью, аппаратным усреднением сигнала под зондом [2]), обладает также существенными недостатками:

– большим (порядка 100…1000 мс) временем установления выходного сигнала, определяемым необходимостью интегрирования сигнала низкой звуковой частоты;

– невозможностью сканирования поверхности исследуемого объекта в непрерывном режиме;

– ограниченной разрешающей способностью в режиме сканирования, связанной с необходимостью анализа пространственного распределения поверхностного потенциала по набору дискретных точек при достаточно большом времени измерения в каждой точке.

Метод невибрирующего конденсатора (зонда Кельвина) является разновидностью метода Кельвина, позволяющей обойтись без вибраций одной из пластин конденсатора, и за счет этого обойти ограничение, накладываемое частотой вибрации на время установления выходного сигнала измерительного преобразователя. Перемещение зонда с высокой скоростью параллельно поверхности образца позволяет получить малое время ее сканирования, что, в свою очередь, обеспечивает условия для повышения разрешающей способности за счет уменьшения геометрических размеров зонда.

Как известно, обобщенное выражение для тока в цепи содержащей конденсатор Кельвина, имеет вид:

,

(1)

где U_CPD – контактная разность потенциалов между зондом Кельвина и исследуемой поверхностью;

С – емкость динамического конденсатора.

Выражение содержит два члена, каждый из которых зависит как от геометрических параметров (емкость С), так и от собственно измеряемого электрического потенциала U_CPD. Для того, чтобы определить условие разделения измеряемых параметров, можно обратиться к методологии многопараметрических измерений параметров объектов [3].

Пусть объект характеризуется p независимыми информативными пара-метрами. Значение некоторой измеряемой величины x_i будет определяться значениями других параметров объекта измерений и влияющих величин ξ_k, в соответствии с математической моделью объекта измерений

.

(2)

Взаимодействие объекта и чувствительного элемента средства измерений характеризуется тем, что на вход первичного преобразователя средства измерений воздействует сигнал X, также определяемый математической моделью объекта измерений

(3)

где F – некоторый функционал, описывающий ряд определенных математических операций, производимых над измеряемыми величинами x_i.

Выходной сигнал Y, формируемый в результате базового измерительного преобразования F сигнала X, содержит информацию об измеряемых физических величинах

(4)

Для обеспечения возможности измерений некоторой величины x_iнеобходимо подвергнуть базовый измерительный сигнал преобразованию Ф_i, которое должно удовлетворять требованию

(5)

Значение измеряемой величины x_i получают в результате обратного измерительного преобразования

(6)

Частным случаем выполнения условия (5) является полное разделение измеряемых физических величин в математической модели базового измерительного сигнала

(7)

Любую из измеряемых физических величин можно рассматривать как параметр состояния объекта измерений S и в этом случае критерием применимости адаптивных методов измерений к рассматриваемому объекту и его свойствам является следующее:

Выбор параметра состояния объекта измерений и его независимое определение с использованием измерительного сигнала базового метода измерений возможно в том случае, когда математическая модель измерительного сигнала допускает аддитивное разделение физической величины, характеризующей этот параметр, относительно остальных параметров объекта измерений.

(8)

Достаточным условием выполнения данного критерия является равенство нулю смешанных частных производных измерительного сигнала

(9)

Это положение выступает в качестве критерия соответствия физического явления или эффекта, возникающего при взаимодействии объекта измерений и чувствительного элемента первичного измерительного преобразователя, процедуре односигнальных адаптивных измерений.

Рассмотрим возможности введения такого разделения в случае невибрирующего конденсатора.

Второй член выражения (1) равен нулю при использовании классического метода Кельвина, т.е. полагается, что потенциал между пластинами конденсатора не изменяется в процессе измерений. Тогда , а ток в цепи обеспечивается только изменением емкости конденсатора:

(10)

Если же мы будем сканировать контролируемую поверхность невибрирующим зондом то, в общем случае, ни одна из производных в выражении (1) не может быть приравнена к нулю. Следовательно, на этапе планирования эксперимента необходимо найти воздействие, обнуляющее один из множителей перед производными, и не обнуляющее другой.

При сканировании поверхности образца невибрирующим зондом последний движется вдоль поверхности с постоянной скоростью и на постоянном расстоянии от нее (рисунок 1). В этом случае изменение выходного сигнала электрометрического зонда связано с пространственным распределением геометрических параметров и КРП поверхности соотношением

.

(11)

Рисунок 1 – Схема реализации метода невибрирующего конденсатора.

В этом случае разделение геометрической и потенциальной составляющих может производиться путем сведения к нулю измеряемого значения контактной разности потенциалов U_CPD в соответствии с критерием (9). Последнее может быть осуществлено подачей внешнего потенциала U_bias, который влияет только на геометрическую составляющую, оставляя неизменной потенциальную.

Литература:

1. Zisman, W.A. A new method of measuring contact potential differences in metals // Review Of Scientific Instruments. – 1932. – V. 3. – P. 367.

2. Zharin, A.L. Contact Potential Difference Techniques as Probing Tools in Tribology and Surface Mapping // Applied Scanning Probe Methods. – 2010. – V. 14. – P. 687-720.

3. Воробей, Р.И. Методология и средства измерений параметров объектов с неопределенными состояниями / Воробей Р.И., Гусев О.К., Жарин А.Л., Свистун А.И., Тявловский А.К., Тявловский К.Л. – Минск: БНТУ, 2009. – 586 с.