Современные информационные технологии/2.Вычислительная техника и программирова­ние

 

С.Н. Данилин, М.В. Макаров, С.А. Щаников

Муромский институт Владимирского государственного университета

602245, г. Муром, Владимирской обл., ул. Орловская, 23

E-mail: nauka-murom@yandex.ru

Преобразование систем координат с использованием нейросетевых алгоритмов

 

Новые алгоритмы обработки информации имеют практическую ценность             в том случае, если они  отличаются от известных: а)  меньшей погрешностью; б) лучшим быстродействием; в) реализуются меньшими программно-аппаратными средствами.  Принятие в науке нейросетевой парадигмы позволяет строить алгоритмы решения  многих практических задач на принципиально новом уровне по всем выше названным показателям.

 Рассмотрим в качестве примера преобразование координат из полярной системы координат в декартовую:

                                                (1)

Известные решения данной задачи основаны на использовании различных вариантов разложения тригонометрических функций в ряды. Наиболее «узким местом» в этом случае (при заданной погрешности) является время преобразования, большая часть которого приходится  на вычисление тригонометрических функций [1].

Предположение об эффективности решения задачи преобразования координат нейросетевыми алгоритмами основано на том обстоятельстве, что нейронные сети являются наилучшим аппроксиматором функций [2]. Отличительной особенностью решения задач в нейросетевом базисе является комплексный подход к задаче в целом без разделения на частные подзадачи. Нейронная сеть позволяет осуществлять совместное преобразование координат, схематично показанное на рисунке 1.

Рисунок 1 – Совместное преобразование координат.

Рассмотрим преобразование в первом квадранте декартовой системы координат в диапазоне изменения каждой из координат от 0 до 1 (рисунок 2). Общее количество точек, используемых при переводе из полярной                      в декартовую систему координат, составляет 100 (на рисунке 2 номера некоторых точек показаны курсивом). Входным сигналом нейронной сети является массив , состоящий из координат точек в полярной системе координат, а выходным сигналом – массив такой же размерности, состоящий из координат тех же точек в декартовой системе.

Рисунок 2 – Точки, используемые для обучения нейронной сети.

В качестве инструментального средства исследований использовался пакет прикладных программ Neural Network Toolbox версии 4, функционирующий под управлением ядра системы Matlab версии 6.1 [3].

В процессе исследований синтезировались простейшие двухслойные нейронные сети прямого распространения с полными связями. В процессе предварительного анализа были выбраны следующие функции активации: для первого слоя – сигмоидная функция

для второго слоя – линейная функция

Процесс обучения нейронных сетей связан с такой настройкой ее весов              и смещений, чтобы минимизировать функционал, зависящий от ошибок сети, то есть разности между требуемым и реальным сигналом на ее выходе.                    В качестве такого функционала использована сумма квадратов отличий реальных значений координат и координат, полученных с помощью              нейронной сети:

В качестве алгоритма обучения использовался алгоритм Левенберга-Марквардта, дополненный регуляризацией по Байесу. Данный алгоритм находит широкое применение при решении задач аппроксимации нелинейных зависимостей. Он выполняет процедуру обучения, если функции взвешивания, накопления и активации имеют производные. В отличие от других алгоритмов здесь используется метод регуляризации, который позволяет успешно справится с проблемой переобучения путем минимизации комбинированного функционала качества обучения, учитывающего не только сумму квадратов ошибок обучения, но и квадраты весов. Для вычисления якобиана функционала качества по переменным веса и смещения применен метод обратного распространения ошибки.

Исследуемая структура нейронной сети представлена на рисунке 3, а ее математическое выражение может быть записано следующим образом:

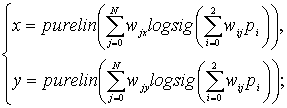
где

Синтезированная нейронная сеть с пятью нейронами в первом слое и двумя во втором обеспечивает погрешность менее , что уже лучше погрешности алгоритмов (), построенных по классической схеме преобразования координат [1].

Рисунок 3 – Топология нейронной сети.

Использование семи нейронов в первом слое позволяет снизить погрешность преобразования еще более чем в 10 раз (рисунки 4 и 5) и достичь результата порядка . При этом следует отметить, что даже такой хороший результат может  оказаться не предельно достижимым, поскольку существует значительная вероятность того, что при обучении нейронная сеть попала лишь в локальный минимум функционала оптимизации, поскольку достижение глобального минимума является отдельной сложной задачей, выходящей за рамки данного исследования.

Рисунок 4 – Погрешность преобразования по координате x.

Рисунок 5 – Погрешность преобразования по координате y.

Еще одним важным преимуществом нейросетевого преобразователя координат является резкое сокращение времени преобразования. По результатам работы [1] можно сделать вывод, что при реализации преобразования (1) для вычислителей классической фон-неймановской архитектуры потребуется как минимум 15 машинных операций (10 умножений и 5 сложений). Следовательно, минимальное общее время преобразования составит 15 машинных циклов, которые выполняются последовательно. При реализации синтезированной нейронной сети на нейровычислителях время преобразования составит всего два (!) машинных цикла.

По мнению авторов, достигнутого значения точности преобразования более чем достаточно для большинства практических применений. В случае необходимости, ее дальнейшее улучшение легко осуществить путем увеличения числа нейронов в первом слое, при этом аппаратные затраты возрастают незначительно, а время преобразования остается прежним. Сравнение стоимости реализации классического и нейросетевого вычислителей не выявило существенной разницы между ними.

Таким образом, предлагаемый нейросетевой алгоритм значительно превосходит по своей эффективности известные, построенные по традиционной схеме. Достигнутый результат является еще одним подтверждением того, что            в настоящее время нейрокомпьютерам нет равных по критерию «цена-качество» [4].

 

 

Литература

1. Пантелеев С.В., Данилин С.Н., Яковлев А.А. Оптимизация алгоритмов обработки цифровой информации. // Тезисы докладов 3-й Международной конференции и выставки «Цифровая обработка сигналов и ее применение». – М.: ИПУ, 2000. Часть 1. – С. 169-172

2. Нейроматематика. Кн. 6: Учеб. пособие для вузов. / Под ред. А.И. Галушкина. – М.: ИПРЖР, 2002. 448 с. (Серия Нейрокомпьютеры и их применение).

3. Медведев В.С., Потемкин В.Г. Нейронные сети. MATLAB 6. / Под общ. ред. В.Г. Потемкина. – М.: ДИАЛОГ-МИФИ, 2008. – 496 с.

4. Нейрокомпьютеры. Кн. 3: Учеб. пособие для вузов. / Общ. ред. А.И. Галушкина. – М.: ИПРЖР, 2000. 528 с. (Серия Нейрокомпьютеры и их               применение).