Физика/2.Физика твердого тела

 

Д. ф.-м. н. Жуков Е. А.[1], к. ф.-м. н. Каминский А. В.[1],

к. ф.-м. н. Жукова В. И.[2]

 

1. Тихоокеанский государственный университет, Россия

2. Дальневосточный государственный университет путей сообщения, Россия

Метод определения упругих и магнитоупругих констант магнитных кристаллов

 

         Развитие информационно - телекоммуникационных систем в последние десятилетия характеризуется процессом миниатюризации электронной компонентной базы вплоть до нанометрового диапазона, ростом частоты переключения до единиц терагерц. При этом основой многих из устройств стали пластины и стержни магнитных кристаллов [1, 2]. Для достижения заданных свойств элементы создаются из слоев различных кристаллов [3-5] или из кристаллов с частично замещенными ионами (например, редкоземельный ион в ортоферритах частично заменяется ионом висмута [6]). Скорость срабатывания этих устройств определяется динамикой магнитной подсистемы, которая взаимодействует с акустической подсистемой. Для учета этого взаимодействия необходим контроль за магнитными, упругими и магнитоупругими константами гетеростуктур.

         В настоящей работе предложен метод измерения магнитных, упругих и магнитоупругих констант магнитных кристаллов. Метод основан на измерениях зависимостей резонансных частот изгибных колебаний пластин от магнитного поля.

         Согласно [7] закон дисперсии изгибных колебаний ферро и антиферромагнитных пластин, ограниченных вдоль кристаллографической оси C при направлении магнитного поля, магнитного момента и волнового вектора вдоль кристаллографической оси A выглядит следующим образом

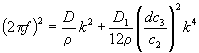                             ,                        (1)

где f – частота, r – плотность, k – волновое число, d – толщина пластины. Рассмотрим легкоплоскостные антиферромагнетики со слабым ферромагнетизмом и малой анизотропией в базисной плоскости. В этом случае [7]:

; ;

; ; ;

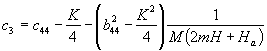сik, bik – упругие и магнитоупругие константы, m – единичный вектор намагниченности, M – магнитный момент подрешеток; K = MHa – константа анизотропии, Ha – поле анизотропии.

         В отсутствии внешнего магнитного поля (H = 0) закон дисперсии квадратичный, (f ~ k2, D = 0), как и для пластин немагнитных кристаллов. Согласно [7], магнитное поле придает дополнительную поперечную жесткость, в законе дисперсии появляется слагаемое, соответствующее объемному звуку. В результате характер дисперсионной зависимости для изгибных колебаний становится промежуточным между квадратичным и линейным.

         Упругие константы по порядку величины сik ~ 1011 эрг/см3, магнитоупругие константы bik и константа анизотропии K значительно меньше (для гематита и бората железа, например  ~ 106 эрг/см3). Малость констант bik и K по отношению к сik позволяет представить зависимость (1) в линеаризованной форме

                                   ,                                                           (2)

где

, ,

, – предельные частоты при и , соответственно:

;      .

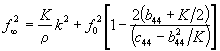что позволяет, используя  метод наименьших квадратов, определить комбинации магнитных, упругих и магнитоупругих параметров , и .

         Используя образцы пластин, вырезанные в разных кристаллографических плоскостях и возбуждая изгибные колебания с различными направлениями волнового вектора, можно получить систему уравнений для соответствующих комбинаций , из которых можно определить упругие константы. Используя эти константы, можно из сиcтемы уравнений для , определить магнитоупругие константы.

         Таким образом, предложенная методика позволяет определять упругие, магнитоупругие и магнитные константы. При этом результаты измерений являются чувствительными к качеству обработки только двух поверхностей, ограничивающих пластину (в нашем случае вдоль оси С) и не зависят от размеров и формы образцов по другим координатам. Это выгодно отличает предложенную методику от традиционной, в которой измерения проводятся на образцах, грани которых обработаны со всех сторон [8]. Последнее свойство может стать незаменимым при измерении констант наноразмерных гетероструктур.

         Работа выполнена при поддержке Минобрнауки РФ в рамках аналитической ведомственной целевой программы «Развитие научного потенциала высшей школы» (проект № 2.1.1/11383).

 

Литература:

1.      Голенищев-Кутузов А. В., Голенищев-Кутузов В. А., Калимуллин Р. И. Индуцированные доменные структуры в электро и магнитоупорядоченных веществах. – М.: Физматлит, 2003.

2.      Mostovoy M. Multiferroics go high-Tc / Nature materials.  2008.  V. 7.  N. 4.

3.      Rijnders G., Blank Dave H. A. An atomic force pencil and eraser // Ibidem.

4.      Cen C., Thiel S., Hammerl G., Schneider C. W., Andersen K. E., Hellberg C. S., Mannhart J., Levy J. Nanoscale control of an interfacial metal-insulator transition at room temperature //  Ibidem.

5.      Palkar V. R., Prashanthi K. Observation of magnetoelectric coupling in Bi0.7Dy0.3FeO3 thin films at room temperature // Appl. Phys. Lett.  2008. V. 93. N. 13.

6.      Гуляев Ю. В., Дикштейн И. Е., Шавров В. Г. Поверхностные магнитоакустические волны в магнитных кристаллах в области ориентационных фазовых переходов // УФН. 1997.  Т. 167.  № 7.

7.      Bar’yakhtar V. G., Chetkin M. V, Ivanov B. A., Gadetskii S. N. Dynamics of Topological Magnetic Solitons. Experiment and Theory. – Berlin. : Springer-Verlag, Springer Tracts in Modern Physics.  1994.  V. 129.

8.      Burzo E. Magnetic Properties of Non-Metallic Inorganic Compounds Based on Transition // Landoldt-Börnstein. Elements Numerical Data and Functional Relationships in Science and Technology / Edited by K.-H. Hellwege. – Berlin.: Springer-Verlag,  New Series, Group III: Solid State Physics. – 1993. – V. 27h.