Моделирование потенциальной ямы в
коаксиальном магнитоплазменном ускорителе
Коаксиальный магнитоплазменный ускоритель
является электроэрозийным ускорителем, так как рабочий материал нарабатывается
электроэрозийным путем с поверхности ускорительного канала.
Магнитное поле плазменного укорителя можно
представить как суперпозицию независимых ортогональных полей создаваемых
плазменным шнуром 
(аксиальное поле) и
индуктором 
.
Поскольку нас интересует поле в области ограниченным электродным
стволом, то поле индуктора в этой области можно считать однородным не зависящем
от координат, и имеющем только 
– компоненту 
. Напомним, что линии равного векторного потенциала 
есть, силовые линии
магнитного поля. Кроме магнитных полей имеется и электрическое поле электродной
системы ствол-жгут определяемое выражениями:
Компоненты по осям 
и 
будут соответственно:
Для ограничения траектории движения частиц
в пределах ствола введена потенциальная функция 
– “потенциальная яма”
имеющая аналитический вид:
,
и ее силовая функция, которая определяется выражением:
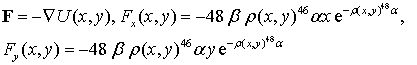
Входящие безразмерные коэффициенты имеют
значения: 
.
Пространственный вид потенциальной функции
и силового поля представлены на рисунках 1 и 2.
а) б)
Рис.1. а) пространственное
распределение потенциальной ямы 
; б) силовое поле 
а) б)
Рис.2. Компоненты градиента
потенциальной функции 
:
а) по оси 
; б) по оси 
На основе полученных соотношений запишем
уравнение динамики заряженных частиц в электромагнитных полях в векторной форме
[1]:
.
Далее уравнение динамики заряженных частиц
решалось с помощью дифференциальных уравнений первого порядка методом
Рунге–Кутта с фиксированным шагом с числом дискретизации 
. Все частицы имели одинаковую массу, заряд (+) и продольную
компоненту скорости. Начальные значения поперечных скоростей и исходных
координат частиц задавались различные. Относительные значения поперечных
скоростей и координаты по отношению к радиусу электрода приведены на рисунке 3.
Из картины видно, что при больших поперечных скоростях получаются большие
радиусы. При заданной конфигурации электромагнитного поля частицы движутся по
спирали.
а) б) в)
Рис.3. а) начальные положение
координат и поперечные величины и направления скоростей;
б) проекция траектории частиц на плоскость x, y;
в) вид пространственной
траектории частиц
Траектория,
усредненная по Ларморовскому периоду, тоже представляет собой спираль более
низкой частоты [2]. Таким образом, при распространении частиц, центр
окружности, по которой вращаются частицы в поперечной плоскости, движется по
низкочастотной спирали. Соприкасаясь со стенками, частицы вызывают эрозию, в
результате которой изменяется масса плазмы. То есть, масса пучка меняется по
колебательному закону.
Таким образом, представлен промежуточный
этап разрабатываемой математической модели коаксиального магнитоплазменного
ускорителя.
Список литературы
1. Ландау Л.Д., Лифшиц Е.М.Теоретическая
физика Т. 2: Теория поля. – М.: Наука, 1992.
– 664 с.
2.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика Т. 8: Электродинамика сплошных сред. – М.: Наука, 1992. – 664 с.