Замковая Л.Д.
Национальный горный
университет (Украина)
О
практической устойчивости решений суммарно-разностных уравнений
Введение.
Математической
моделью динамики некоторых механических, экологических и других систем,
состояния которых изменяются в дискретные моменты времени, являются
конечноразностные уравнения. Важное место при качественном анализе поведения
решения таких систем вместе с устойчивостью по Ляпунову занимает свойство
практической устойчивости [6]. В работах [2; 5, с. 297-303; 7] основным методом
исследования практической устойчивости дискретных систем является второй метод
Ляпунова и, соответственно, результаты сформулированы в терминах функций
Ляпунова. В статьях [1, 2] изучено влияние импульсных возмущений некоторого
вида на практическую устойчивость решений нелинейной дискретной системы.
Настоящая работа
посвящена построению достаточных условий практической устойчивости решений
нелинейных дискретных систем, содержащих комбинации степенных и суммарных
возмущений, при условии, что известны свойства решений системы линейного
приближения. При этом используется дискретный аналог формулы Коши и теория
дискретных неравенств.
Постановка
задачи. В 
-мерном векторном пространстве 
рассматриваются конечноразностные
системы
(1)
и возмущенная
. (2)
Здесь: t –
дискретное время; 
; 
; 
– множество начальных моментов; 
; 
– 
матрица; 
; 
.
Предполагается, что система (2) имеет единственное решение 
, удовлетворяющее условию 
и существующее при
всех 
.
Относительно невозмущенной системы (1) и возмущения 
делаются следующие
предположения.
Предположение 1. Матрица Коши 
, 
, системы (1) удовлетворяет оценке
(3)
с
некоторыми положительными функциями 
и 
.
Предположение 2. Вектор-функции 
и 
в области 
удовлетворяют
неравенствам
, (4)
, (5)
где 
, 
, 
, 
– неотрицательные
функции. Здесь и далее 
– любая векторная
норма в 
.
Будем изучать практическую устойчивость в смысле определения, приведенного
в [6].
Нулевое решение 
системы (2)
называется 
практически
устойчивым, где 
, если для любого решения 
этой системы
справедлива оценка 
при 
, как только 
.
Цель данной
работы:
установить достаточные условия 
практической
устойчивости нулевого решения системы (2) при предположениях 1 и 2.
Основные результаты. Введем обозначение
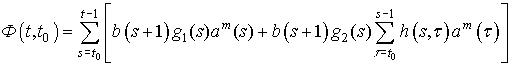. (6)
Теорема 1. Пусть:
1) выполняются предположения 1 и 2, где 
;
2) существуют величины 
и 
такие, что 
; 
, где 
определено в (6);
3) величины 
и 
, 
, удовлетворяют соотношению
.
Тогда нулевое решение 
системы (2) 
практически
устойчиво.
Доказательство. Всякое решение 
, 
, системы (2) удовлетворяет уравнению
. (7)
В это уравнение подставим оценки (3)-(5) и полученное неравенство
преобразуем к виду
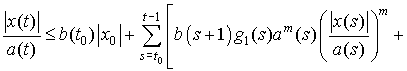
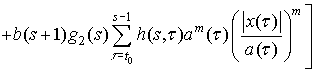. (8)
Оценивая решение дискретного неравенства (8) при 
согласно [8, лемма
2.2., 
], получаем следующую оценку решения 
системы (2):
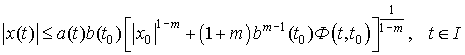. (9)
Из неравенства (9) и условия 2) теоремы следует
,
где 
. Функция 
монотонно возрастает
по второму аргументу. Выбрав начальные
возмущения из области 
, с учетом условия 3), получаем
.
Теорема
1 доказана.
Теорема
2. Пусть:
1) выполняются
предположения 1 и 2, где 
;
2)
выполняется условие 2) теоремы 1;
3) 
, (10)
где
; (11)
4) величины 
и 
, 
, удовлетворяют соотношению
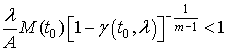. (12)
Тогда нулевое
решение 
системы (2) 
практически
устойчиво.
Доказательство. Будем исходить из
неравенства (8), которое было получено с применением только предположений 1 и
2, где нет ограничений на показатель 
. При 
из неравенства (8) на
основании [8, лемма 2.2, 
] следует такая оценка решения 
системы (2):
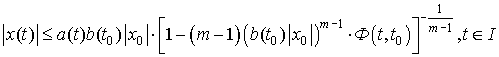, (13)
при условии, что выражение в
квадратных скобках положительно; 
определено в (6).
Отсюда с учетом условия 2) теоремы 2 и обозначения 
(11) получаем
, (14)
если 
. Пусть теперь 
. Тогда в силу (11) и (10) имеем: 
, т.е. при 
справедлива оценка
(14). Из неравенства (14) и условия (12) теоремы 2 получаем, что если 
, то
.
Теорема 2
доказана.
Теорема 3. Пусть:
1) выполняются
предположения 1 и 2, где 
;
2) существует 
такое, что
,
где
; (15)
3) величины 
и 
, 
, связаны неравенством
.
Тогда нулевое
решение 
системы (2) 
практически
устойчиво.
Доказательство. Из неравенства (8) при 
, используя [4, с. 26, лемма 4], получаем такую оценку
решения 
системы (2):
,
где 
определено в (15). Из
этой оценки выводим утверждение теоремы.
Анализ
полученных результатов. Если в системе (2) 
, т.е. суммарные возмущения отсутствуют, то теоремы 1-3
являются дискретными аналогами соответственно теорем 1.8.А, 1.9.А, 1.10.А из
[3] для дифференциальных систем. Из теоремы 3 при 
следует теорема 4.3
из [6].
Результаты
статьи можно использовать для нахождения областей практической устойчивости
динамических систем, математическими моделями которых могут служить
суммарно-разностные системы (2)-(5). Дальнейший интерес представляет построение
достаточных условий практической устойчивости решений систем конечноразностных
уравнений как с суммарными возмущениями других видов, так и при других
предположениях относительно решений невозмущенной системы (1).
Литература
1.
Абдуллин
Р.З. Устойчивость разностных уравнений с импульсным воздействием // Автоматика
и телемеханика. – 1995. – №1. – С. 107–116.
2.
Абдуллин
Р.З. Метод сравнения в устойчивости нелинейных разностных уравнений с
импульсными воздействиями // Автоматизация и телемеханика. – 2000. – №11. – С.
44–56.
3.
Борисенко
С.Д., Косолапов В.И., Оболенский А.Ю. Устойчивость процессов при непрерывных и дискретных возмущениях. – К.:
Наук. думка, 1988. – 200 с.
4. Быков Я.В., Линенко В.Г. О некоторых вопросах качественной теории
систем разностных уравнений. – Фрунзе: "Илим", 1968. – 139 с.
5. Мартынюк А.А. Устойчивость движения сложных систем. – К.: Наук.
думка, 1975. – 352 с.
6. Мартынюк А.А. Анализ устойчивости дискретных систем // Прикладная
механика. – 2000. – 36, №7. – С. 3–35.
7. Michel A.N., Wu S.H. Stability of discrete
systems over finite interval time // Int. J. Control. – 1969. v. 9. – P.
679–693.
8. Talpalaru P. Stability problems for
difference equations // An. Sti. Univ. "Al. I. Cuza" Jasi. Mat. –
2005. – 51, №2. – P. 231–244.