Технические науки

Электротехника и радиоэлектроника

В.С. Тверезовский, Р.В. Бараненко

Херсонский национальный технический университет

ОПТИМИЗАЦИЯ РАБОТЫ
ВЫЧИСЛИТЕЛЬНОГО УСТРОЙСТВА

Постоянное развитие средств измерений и контроля различных параметров изделий и процессов является неотъемлемой частью научно-технического прогресса. Одной из основных задач при разработке измерительных систем является повышение точности, быстродействия и увеличение диапазона измеряемых величин [1].

В настоящее время известно вычислительное устройство [2], недостатками которого являются низкая точность и ограниченные функциональные возможности, т.к. оно позволяет выполнять только одну операцию умножения сигналов.

Этих недостатков лишено вычислительное устройство [3], однако и оно выполняет только две операции: умножения и деления входных напряжений.

Целью работы является расширение функциональных возможностей устройства, за счет выполнения дополнительных операций возведения в квадрат и извлечения квадратного корня.

Поставленная цель достигается тем, что разработанное авторами устройство [4] дополнительно содержит схему сравнения, последовательно соединенные генератор линейно изменяющегося напряжения и ключ, коммутатор, выход которого соединен с одним выводом элемента с управляемым коэффициентом передачи первой цепочки, второй вывод которого соединен с первым входом схемы сравнения, второй вход которой соединен с первым входом устройства, а выход через ключ соединен с входом усилителя, второй вход устройства соединен с одним выводом элемента с управляемым коэффициентом передачи второй цепочки и первым входом коммутатора, второй вход которого соединен с другим выводом элемента с управляемым коэффициентом передачи второй цепочки, а третий вход коммутатора является третьим входом устройства, другие выводы масштабных резисторов соединены с шиной нулевого потенциала.

На рис. 1 показана структурная схема устройства. Оно содержит генератор линейно изменяющегося напряжения 1, ключ 2, усилитель 3, обладающий свойством запоминания выходного напряжения, элементы с управляемым коэффициентом передачи 4 и 5, коммутатор 6, схему сравнения 7, масштабные резисторы 8, 9, клеммы входных сигналов 10,11, 12, клеммы выходных сигналов 13, 14.

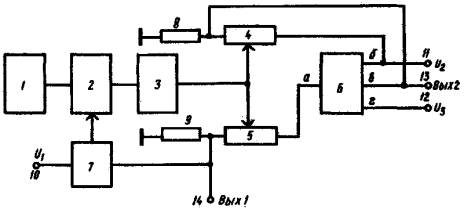
Рис. 1 Структурная схема вычислительного устройства

В схеме масштабные резисторы 8 и 9 имеют одинаковые номиналы и подобраны с высокой точностью, а управляемые сопротивления также имеют идентичные передаточные характеристики.

В исходном состоянии генератор линейно изменяющего напряжения 1 периодически вырабатывает импульс плавно изменяющегося напряжения, ключ 2 закрыт потенциалом, поступающим со схемы сравнения 7, на выводах устройства сигналы отсутствуют.

Рассмотрим работу устройства при возведении в квадрат и делении.

На входы 10 и 11 подаются напряжения соответственно, коммутатор 6 коммутирует цепь. Ключ 2 открывается и изменяющееся напряжение через него поступает на вход усилителя 3, который своим выходным сигналом воздействует на управляемые сопротивления 4 и 5, плавно их уменьшая. На выходах делителей, образованных масштабными резисторами 8 и 9 и элементами с управляемым коэффициентом передачи 4 и 5, будут изменяющиеся напряжения

,

где - сопротивления элементов 4, 5;

- сопротивления масштабных резисторов 8 и 9 соответственно.

Так как, то .

Очевидно, настучит момент, когда будет выполняться условие

.

(1)

При наступлении этого момента, схема сравнения вырабатывает потенциал, при котором ключ 2 закроется. Усилитель 3 будет хранить напряжение, которое действовало на его входе в момент наступления равенства (1) (для выполнения операции запоминания достаточно в качестве входного каскада поставить последовательно включенные диод и емкость, а усилитель должен иметь большое входное сопротивление).

Очевидно, на время запоминания усилителем выходного напряжения, коэффициент передачи делителей, образованных также будут постоянными.

После наступления равновесия коммутатор коммутирует цепь ав. На вход делителя, образованного и будет поступать напряжение

.

(2)

На выходной клемме 14 будет напряжение:

.

или с учетом (2)

.

Но , следовательно

,

где .

Следовательно , т.е. устройство позволяет возводить в квадрат напряжение и результат делить на другое входное напряжение.

Если взять постоянным, то устройство возводит в квадрат входное напряжение .

При устройство позволяет получить обратную величину .

При извлечении квадратного корня устройство работает следующим образом.

Исходное состояние схемы такое же, как и в предыдущем случае. Коммутатор коммутирует цепь ав.

Работает схема так же, как и в первом случае до наступления момента равновесия, для которого будут справедливы равенства

.

Из этих уравнений можно записать выражение

.

(3)

После равновесия коммутатор, переключаясь, коммутирует цепь аг. При этом будет выполняться условие . Но из (3) , следовательно, , т.е. устройство делит два входных напряжения, извлекает квадратный корень из результата и умножает все это на третье входное напряжение. При устройство извлекает квадратный корень из входного напряжения. При устройство извлекает квадратный корень из величины обратной входному напряжению. Умножение и деление устройство производит следующим образом.

Исходное состояние такое, как в первом случае.

При равновесии схемы выполняется условие

.

(4)

После этого коммутатор коммутирует цепь аг. Очевидно, для этого случая будет справедливо равенство:

,

следовательно , т.е. устройство умножает два входных напряжения и делит на третье напряжение. При устройство делит два напряжения.

Операцию умножения и деления можно выполнить и другим способом. Для этого необходимо коммутатор поставить в положение аг. После уравновешивания схемы можно записать два уравнения:

.

Из первого уравнения значение подставим во второе, после чего , т.е. устройство умножает два напряжения и делит на третье.

Разработанное вычислительное устройство значительно превосходит известные вычислительные устройства в отношении функциональных возможностей.

Литература:

1. В.С. Тверезовський, Р.В. Бараненко Принцип здійснення гнучкого програмного керування елементами вимірювальних систем за аналізом їх експоненціальних параметрів //Вестник Херсонского государственного технического университета. – 2003. – №2 (18). – С.297-301.

2. Авторское свидетельство СССР №226288, кл. G06G7/16.

3. Патент США №3423579, кл. 235-194, 1969.

4. Авторское свидетельство СССР №641458 «Вычислительное устройство». Автор: В.С. Тверезовский. - Опубл. 05.01.1979, Бюл. №1. - М. Кл.² G06G7/12.