Технические науки/11.Робототехника

К.т.н., доцент Эттель В. А., Глушко И. В.

Карагандинский государственный технический университет, Казахстан

Динамика приводов и учет упругой податливости элементов манипулятора

При исследовании динамики манипуляторов составляют расчетную динамическую модель, учитывающую не только геометрические размеры звеньев и распределение кинематических пар, как при составлении кинематической модели, но и распределении масс звеньев и других элементов манипулятора, участвующих в движении. Могут быть учтены и другие свойства манипулятора, например упругие свойства его элементов. В этом случае число степеней свободы системы становится больше числа степеней подвижности манипулятора, которое определяют как число независимых управляемых движений манипулятора (для манипуляторов с разомкнутой кинематической цепью оно равно числу приводов).

Основные элементы приводов роботов - исполнительные двигатели и механические передачи, связывающие двигатели со звеньями манипулятора. При проектировании передач, а также звеньев самого манипулятора обычно стремятся удовлетворить требованиям высокой жесткости элементов. Однако не всегда удается уменьшить упругую податливость элементов до значений, при которых ее влияние становится несущественным, и прежде все из-за жестких ограничений на массу и габаритные размеры элементов манипулятора.

Податливость элементов приводит к появлению в процессе движения упругих колебаний манипулятора и его рабочего органа. Упругие колебания отрицательно сказываются на работе робота, вызывая увеличение динамических нагрузок на элементы, снижение быстродействия и точности при отработке программных движений, появление незатухающих вибраций, опасных резонансных явлений и.т.п. Поэтому на начальных этапах проектирования целесообразно учесть упругую податливость элементов. Рассчитать возможные амплитуды и частоты упругих колебании и, если они не удовлетворяют требованиям, скорректировать конструкторские решения.

Рассмотрим две простейшие расчетные модели, характерные для роботов. Первая модель (рис. 1а) учитывает сосредоточенную в шарнире упругую податливость передачи, связывающей двигатель со звеном манипулятора. Вторая модель (рис. 1б) учитывает распределенную изгибную податливость звена манипулятора. При выборе расчетной модели робота необходимо выделить наиболее податливые элементы, например выходные валы редукторов, длинные звенья, тросы и т. д., и рассчитать податливость этих элементов по справочникам.  Податливость остальных элементов либо приводят к наиболее податливому участку, либо вообще не учитывают.

J1
 

J2
 
 


J1
 

ρ(x), EI(x)
 

b, c
 
а)                                                               б)

φ1
 

φ2
 

φ
 
 

 


рисунок 1

 

1. Механическую систему «привод-звено манипулятора» во многих случаях можно представить в виде двухмассовой системы (рис. 1а), учитывающей упругую податливость механической передачи, причем чаще всего лишь ее последней ступени.

Рассмотрим, типовой электрический привод, состоящий из двигателя постоянного тока и редуктора. Упругость редуктора определяется в основном упругостью валов, зубьев шестерен, подшипников, шлицевых и шпоночных соединений и т. д. Двигатели постоянного тока обычного исполнения высокооборотные. Максимальные же угловые скорости вращения звеньев манипулятора в среднем составляют π/2 рад/с, что приводит к необходимости использования редукторов с большими передаточными отношениями i (сотни). При этом последняя (считая от исполнительного двигателя) ступень редуктора выполняется с довольно высоким передаточным отношением (десятки). В результате податливость редактора в основном определяется податливостью элементов выходной ступени (на выходном валу наибольший крутящий момент) Это позволяет приближенно считать, что вся упругая податливость редуктора сосредоточена на его выходе.

Если используют специальные высокомоментные двигатели, то для передачи движения от двигателя к звену не требуется длинных кинематических цепей. Однако и здесь можно выделить элементы, которые вносят наибольшим вклад в упругую податливость редуктора.

На основании такого рассмотрения часто можно предельно упростить расчетную модель механической системы привод - звено манипулятора и привести ее к двухмассовой  (рис. 1а). Для нее можно записать систему уравнений:

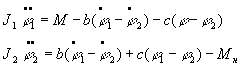                                                                        (1)

где J1 - момент инерции двигателя и механической передачи, приведенные к выходу передачи; φ1 - угол поворота вала двигателя, приведенный к выходу передачи; М - момент, развиваемый  двигателем, приведенный к  выходу передачи; b, с - коэффициент внутреннего вязкого трения и эквивалентная жесткость     передачи,    приведенные    к ее выходу; φ2 - угол поворота звена; J2  -момент инерции звена или последовательности звеньев; Мн - момент нагрузки (например, момент сил тяжести).

Исключая из системы уравнений переменную φ1, получим уравнение относительно переменной φ2 в операторной форме:

          (2)

где  - собственная частота двухмассовой системы; ,  - парциальные частоты; , ,  - показателя затухания колебаний; J=J1 + J2 - суммарный момент инерции системы.

Затухание колебаний, обусловленное наличием сил внутреннего вязкого трения, как правило, не очень велико. Так. для электрических приводов естественное затухание колебаний под действием сил внутреннего трения характеризуется логарифмическим декрементом не более 0,1-0,3. Это приводит к тому, что для нежесткой конструкции в переходных пpoцессах, например при торможении звена вблизи конечного положения, возникают интенсивные колебания, для затухания которых требуется значительное время. В итоге полное время выполнения операции увеличивается.

Для получения числовых оценок можно рассматривать несколько случаев:

1) считая , что собственное демпфирование в механической системе отсутствует (b=0) из уравнения (2) получим операторное уравнение:

2) считая механическую передачу абсолютно жесткой, вместо двухмассовой расчетной модели получим одномассовую, а из системы уравнений 1 при φ1 = φ2 = φ получим одно уравнение . В некоторых случаях двухмассовая расчетная модель оказывается недостаточно точной. Более близкой к реальной системе может оказаться многомассовая расчетная модель.

Однако, упругость может играть и положительную роль. Так, часто в запястье рабочего органа вводят упругость для создания податливости при выполнении сборочных и других операций с объектами внешней среды. Наконец, существуют манипуляторы типа хобота, в которых управляемая гибкость лежит в основе из принципа действия.

 

Литература:

1.Бурдаков С. Ф., В. А. Дьяченко, А. Н. Тимофеев. Проектирование манипуляторов промышленных роботов и роботизированных комплексов: Учебное пособие. Москва «Высшая школа», 1986-264 с.

2. Юревич Е.И. Основы робототехники. – 2-е изд., перераб. И доп. СПб.: БХВ-Петербург, 2005-416 с.