магистр Аллилуйкина А.Д.
Донецкий
национальный технический университет, Украина
Исследование модели ведомого генератора сети синхронизации, построенного
на основе ФАПЧ
Задача о взаимодействии двух и более
генераторов для области радиотехники является традиционной и связана, как правило, с обеспечением синхронных режимов
нескольких колебательных процессов. В последние годы с развитием синхронных
цифровых систем передачи информации цепочки последовательно соединенных
генераторов приобрели новые области применения. В некоторых случаях они
используются для синхронизации работы разнесенных в пространстве
радиотехнических систем. Так, например, в сети передачи данных синхронной
цифровой иерархии (SDH) используется цепь синхронизации, включающая в себя десятки последовательно
синхронизируемых генераторов. [1]
В связи с широким
распространением и важностью цифровых сетей передачи данных, исследования,
посвященные улучшению качества их работы, представляют большой научный и
практический интерес. В том числе важным является вопрос об улучшении качества
сигнала синхронизации. Для решения данного вопроса необходимы исследования
работы как одного генератора,
являющегося частью сети синхронизации, так и цепочки синхронизируемых генераторов.
Целью данной работы является исследование
аналитической и цифровой модели генератора системы синхронизации.
В качестве примера данная задача решается
для синхросигнала с частотой 10МГц. В соответствие с рекомендациями ITU-T данный
сигнал применяется для синхронизации цифрового оборудования.
В качестве примера реализации генератора
сети синхронизации выбираем систему ФАПЧ на основе ИМС 4046(рис.1)

Рисунок 1 – Принципиальная схема ФАПЧ
Аналитическую модель системы представим в
виде передаточных функций. Для этого воспользуемся методикой, приведенной в [2].
а)
передаточная функция разомкнутой системы (рис.2)
Краз(р)=![]() (1)
(1)
б) передаточная функция замкнутой системы
Кзам(р)=![]() (2)
(2)

Рисунок 2 – Структурная схема ФАПЧ
Где КФНЧ(р) –
передаточная функция фильтра, КФд(р) –передаточная функция ФД, КГУН(р)
– передаточная функция генератора, управляемого напряжением.
КФд=Vcc/π
(3)
Определим коэффициент усиления ГУН из формулы (11) [3]:
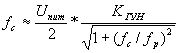
Отсюда:
![]() (4)
(4)
КФНЧ(р)=![]() (5)
(5)
Для исследования устойчивости генератора
сети синхронизации воспользуемся критерием Найквиста.
По
передаточной функции (1) находим
комплексный коэффициент передачи, подставив в (1) p = jω.
Краз=![]() (6)
(6)
Сначала построим годограф частотной
характеристики
![]()
![]() (7)
(7)
Приведем (7) к виду:
![]() (8)
(8)
Для построения годографа частотной характеристики
сначала определим значения U(ω) и V(ω) при ω=
0 і ω=∞.
При ω=0, U(0)=1, V(0)=0.
При
ω=∞, раскрыв неопределенность, получим U(∞)=0 и V(∞)=0.
В
результате годограф частотной характеристики W'(jω) примет вид:

Рисунок 3 – Исследование устойчивости ФАПЧ
Имея годограф частотной
характеристики W'(jω)
(рис.3а), можно построить амплитудно-фазовоую частотную характеристику ФАПЧ W(jω), если учесть (1). В результате получим:
![]() (9)
(9)
![]() (10)
(10)
Для оценки пределов работоспособности
системы построим графики
аплитудно-частотной характеристики
замкнутой системы ФАПЧ для различных значений емкости фильтра: Сф=0,1 мкФ,Сф=1
мкФ, Сф=10 мкФ (рис4).
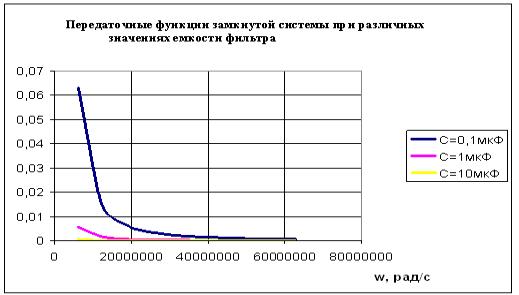
Рисунок
4 – Передаточные функции замкнутой
системы при различных значениях емкости фильтра
Проанализировав, полученные зависимости, можно сделать
вывод, что при увеличении емкости фильтра
уменьшается коэффициент усиления системы.
Рассчитаем частоту среза фильтра (fp) и ширину полосы пропускания. при различных значениях емкости
фильтра:
![]() (11)
(11)
Полученные данные приведены в таблице 1.
Таблица 1
|
Сф,
мкФ |
Частота
среза, КГц |
Полоса
пропускания, Кгц |
|
0,1 |
49 |
98 |
|
1 |
4,9 |
9,8 |
|
10 |
0,49 |
0,98 |
Видно, что по мере увеличения емкости
фильтра сужается полоса пропускания.
Сужение полосы пропускания
приводит к тому, что система становится менее подверженной влиянию шумовых
компонентов. Поведение системы при влиянии шумовых компонентов при разных значения Сф исследовано более обстоятельно с помощью
цифрового моделирования. Цифровая модель системы приведена на рис. 5
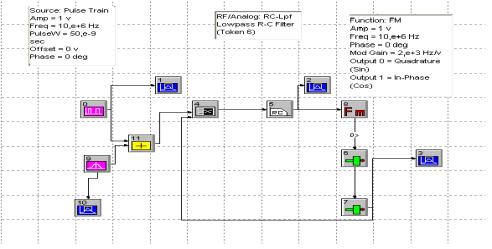
Рисунок 5 – Структурная схема цифровой модели ФАПЧ
Цифровая модель, построенная в
моделирующем пакете System View. В качестве реализации шума был выбран гауссовский
белый шум.

Рисунок 6 –
Перескок фазы в неправильную рабочую точку под влиянием шумовых компонент
Анализ результатов:
1.
Средствами цифрового и
аналитического моделирования показана работоспособность выбранного варианта
построения ведомого генератора сети синхронизации на основе ФАПЧ
2.
Результирующая
амплитудно-фазовая частотная характеристика ФАПЧ W(jω) (рис.3б) пересекает ось абсцисс и в
зависимости от значений параметров отдельных звеньев контура управления точка
пересечения оси расположится либо правее, либо левее точки -1, j0. Таким
образом, ФАПЧ может быть устойчива или неустойчива. Положение точки
пересечения оси зависит, в частотности, от коэффициентов КГУН и КФД .
3.
При увеличении этих
коэффициентов точка пересечения сдвигается влево и при некотором их значении
амплитудно-фазовая частотная характеристика охватит точку -1, j0, а это значит,
что ФАПЧ перейдет в неустойчивое состояние.
4.
В ходе построения
аналитической модели системы ФАПЧ в виде
передаточных функций системы при разных
значениях параметра емкости фильтра Сф была выявлена следующая зависимость, что
с увеличением емкости фильтра уменьшается коэффициент усиления системы. При
увеличении частоты также наблюдается уменьшение значения коэффициента усиления.
5.
Видно, что по мере
увеличения емкости фильтра сужается полоса пропускания. Сужение полосы пропускания приводит к тому, что система становится
менее подверженной влиянию шумовых компонентов. Данное предположение было
подтверждено с помощью цифрового моделирования.
6.
При увеличении емкости
фильтра наблюдается также увеличение времени переходного процесса, это
объясняется тем, что при сужении полосы пропускания время фильтрации
увеличивается, что приводит к увеличению времени переходного процесса во всей
системе.
7.
С другой стороны, при увеличении емкости
фильтра наблюдается уменьшение частоты шумового сдвига системы в неправильную
рабочую точку. Следовательно, для подавление шумовых компонентов, влияющих на
систему и переводящих ее в аварийное состояние, необходимо сузить полосу
пропускания, увеличив емкость фильтра.
Литература:
1. Брени С. Синхронизация цифровых сетей
связи. – М.: Мир, 2003.
2.
Уильрих Л. Роде.
Синтезаторы для микроволновых средств и беспроводной связи.
3.
Методические указания к
выполнению лабораторных работ по системам ФАПЧ. Массачусетский технический
университет.2002.