Технические науки/6. Электротехника и радиоэлектроника

Ивель В.П., Савостин А. А.

Северо-Казахстанский государственный университет

Адаптивная фильтрация электрокардиосигнала

в системе MatLab

Для решения статистических задач подавления помех при стационарных входных сигналах удобным математическим аппаратом является винеровская теория фильтрации. На рис. 1 приведена схема классического винеровского фильтра с одним входом и одним выходом.

Входным (полезным) сигналом устройства является сигнал s[n]. H(z) – дискретная передаточная функция измерительного устройства (ИУ), H_Ф(z) – дискретная передаточная функция адаптивного фильтра (АФ). Выходным сигналом устройства является сигнал ошибки ε[n] = d[n] – y[n]. v[n] – стационарный случайный процесс, некоррелированный с сигналом s[n].

Смысл адаптивной фильтрации заключается в формировании такого сигнала y[n], который бы представлял собой копию сигнала помехи v[n], а фильтр АФ в процессе адаптации должен перестраиваться так, чтобы минимизировать общую мощность выходного сигнала ошибки или минимизировать математическое ожидание квадрата (дисперсию) сигнала ошибки

E_min[ε²] = E[ε²] + E[(v - y)²] + 2E[s(v - y)].

Поскольку s не коррелирован с v и y, получим

E_min[ε²] = E[ε²] + E[(v - y)²].

В идеальном случае E[(v - y)²] = 0, т.е. v = y и сигнал совершенно не искажен помехой.

Процесс адаптации к внешним помехам, заключающийся в подстройке весовых коэффициентов дискретного фильтра, предполагает использование специальных алгоритмов, способствующих достижения экстремума выбранного функционала качества адаптации. В системах компьютерной математики наиболее часто применяются две разновидности алгоритма с использованием образцового сигнала: метод наименьших квадратов (LMS – Least Mean-Square) и рекурсивный метод наименьших квадратов (RLS – Recursive Least Square). В качестве примера предлагается рассмотреть технологию адаптивного подавления шума при записи электрокардиограммы (ЭКГ) с использованием алгоритма RLS, реализованную в системе MatLab.

Предполагается что шум, возникающий при снятии ЭКГ, состоит из помехи с частотой 50 Гц и случайного шума с нормальным (Гаусовым) распределением. Для того чтобы устранить влияние посторонних помех целесообразно измерить эти две составляющие суммарного сигнала без ЭКГ с помощью дополнительного измерительного устройства, а затем полученную информацию использовать в системе адаптивной фильтрации. Хотя этот шум нельзя непосредственно вычесть из электрокардиологического сигнала, поскольку два канала передачи шума (электрокардиограф и дополнительный измеритель) имеют разные характеристики (передаточные функции), однако шумовые случайные процессы, воспринимаемые двумя измерительными устройствами, будут коррелированны между собой и не коррелированны с полезным электрокардиологическим сигналом. Задача решается с использованием пакетов визуального моделирования Simulink и DSP системы MatLab. На рис. 2 представлена Simulink-модель адаптивного подавления помех с использованием RLS-фильтра. Модель содержит следующие блоки.

Блок ECGout является источником нормальной ЭКГ, предварительно записанной в рабочую область.

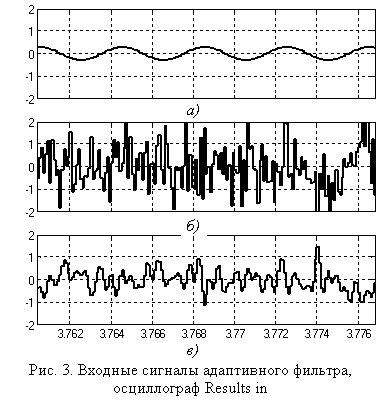Подсистема Noise+50 Hz представляет собой суммарный сигнал от трех блоков (рис. 3, б): источника синусоиды с частотой 50 Гц, источника косинусоиды с частотой 50 Гц (суммарный гармонический сигнал представлен на рис. 3, а) и источника случайного шума с нормальным распределением (Random Noise).

Подсистема FDA Tool Noise Filter содержит нерекурсивный фильтр 32-го порядка и пропорциональное звено с коэффициентом усиления 0,7. На вход этой подсистемы поступает суммарный сигнал помехи (рис. 3, б), а с выхода снимается более низкочастотный сигнал (рис. 3, в). Подсистема имитирует различие характеристик двух измерительных каналов.

Блок RLS Filter, как уже упоминалось, реализует рекурсивный алгоритм наименьших квадратов. При таком алгоритме оценки коэффициентов фильтра можно обновлять для каждого нового полученного набора входных данных без прямого повторного трудоемкого обращения матрицы коэффициентов усиления. Он реализуется с помощью следующих вычислений.

1. Рассчитывается новое значение выходного сигнала фильтра y[n] с учетом новых входных данных u[n] и вычисляется величина ошибки ε[n]:

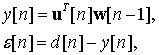
2. Рассчитывается новый вектор-столбец коэффициентов усиления

3. Производится обновление оценки обратной корреляционной матрицы сигнала:

4. Рассчитываются новые значения коэффициентов фильтра

Сигнал ошибки (Error) является разностью зашумленного электрокардиологического сигнала и суммарной помехи или оценкой нормальной ЭКГ. На рис. 4. показаны результаты моделирования.

Сигнал нормальной ЭКГ представлен на рис. 4, а. Зашумленный электрокардиосигнал отображен в следующем окне на рис. 4, б. И, наконец, уже отфильтрованный электрокардиосигнал поступает на третий вход осциллографа Results out (рис. 4, в). Визуальный анализ показывает практически абсолютное сходство исходного и отфильтрованного сигналов.