Технические науки/2. Механика
Ахмедиев С.К., Иманбаева Л.Х., Канатов А.С.,
Ганюков А.А., Безкоровайный П.Г.
Карагандинский государственный технический
университет, Казахстан
Треугольные ячейки в двумерных
задачах механики деформируемого твердого тела
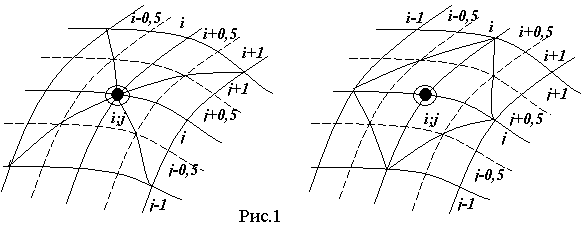
Предлагаются модифицированные криволинейные треугольные ячейки (рис.1) для
двумерных задач механики деформируемого твердого тела применительно к областям
со сложными внутренними и внешними границами. Численные методы, основанные на
сеточной аппроксимации и применяемые к краевым задачам теории упругости в
произвольной области, требуют, чтобы она была близка к действительной. Этого
легче добиться при разбиении области на треугольные криволинейные элементы [1].

Обычно, в методе конечных элементов (МКЭ)
применяются прямолинейные треугольные элементы, напряжения и деформации в них считаются
линейно распределенными по элементам, компоненты вектора смещений относятся к
вершинам элементов. Из-за такого ограничения они не дают реального представления
о напряженно-деформированном состоянии и, в конечном счете, приводят к
искажению точности. Чтобы избежать от таких недостатков, в данном подходе рассматриваются
треугольные криволинейные элементы.
При решении плоской задачи теории упругости,
наложив сетку на рассматриваемую область дискретизируем векторное уравнение
равновесия:
![]() (1)
(1)
Модифицированные криволинейные сетки, имеют
формы треугольников с разными ориентациями. Явное преимущество таких сеток
демонстрируется при дискретизации элементов с различными очертаниями внешних
контуров и внутренних границ. Для этого выбрана местная система координат х1х2, определяющая
координаты каждой точки области. Параметры сетки приняты так, чтобы расстояние
между узлами на координатных линиях, равнялись единице. Искомые функции
определяются в определенных узлах разностной сетки, методом криволинейных сеток
(МКС). Контравариантные компоненты векторов напряжений ![]() определяются в
промежуточных узлах, а компоненты вектора перемещений заданы в основных узлах
разностной сетки. Так как напряжения
определяются в
промежуточных узлах, а компоненты вектора перемещений заданы в основных узлах
разностной сетки. Так как напряжения ![]() определяются в узлах
определяются в узлах ![]() , а
, а ![]() в
в ![]() , то необходимо и все компоненты деформации определять в тех
же узлах:
, то необходимо и все компоненты деформации определять в тех
же узлах:
![]() (2)
(2)
![]() .
.
Сами деформации выражаются через векторы
перемещения и окончательно выглядят, так:
![]() ;
;
![]() ; (3)
; (3)
![]() .
.
По аналогии можно получить выражения
деформации ![]() и
и ![]() [2].
[2].
Последовательно подставляя соотношения (3)
в (2), затем в (1) получаем скалярные алгебраические уравнения в узлах сетки в
перемещениях. Разрешающая система уравнений задачи построена последовательным
обходом узлов сеточной области, наложенный на рассчитываемый объект.
В качестве
примера применения описанного выше методики, для проверки его сходимости и составленной на его основе вычислительной
программы исследован длинный толстостенный круговой цилиндр под действием
внутреннего единичного давления по поверхности отверстия, находящийся в условиях
плоской деформации. Обычно такие задачи встречаются при исследовании напряженного
состояния сосудов высокого давления, используемые в химической промышленности.
Расстояние между центром отверстия и наружной круговой поверхностью составляет
2 радиуса отверстия r=1,0 см. Модуль упругости и коэффициент
Пуассона принимались: Е=100 кПа, ![]() =0,3. Из-за наличия двух осей симметрии, рассматривалась одна
четверть симметрии поверхности отверстия. Исследуемая область разбивалась
равномерно распределенной криволинейной треугольной сеткой. Следует отметить,
что для данной задачи имеется также численное решение, методом граничных
элементов (МГЭ) Бенерджи и Баттерфилда [3].
=0,3. Из-за наличия двух осей симметрии, рассматривалась одна
четверть симметрии поверхности отверстия. Исследуемая область разбивалась
равномерно распределенной криволинейной треугольной сеткой. Следует отметить,
что для данной задачи имеется также численное решение, методом граничных
элементов (МГЭ) Бенерджи и Баттерфилда [3].
Результаты расчетов,
произведенные данной методикой, показывают, что возникшие компоненты напряжения
![]() в сторонах осей
симметрии и компоненты перемещений
в сторонах осей
симметрии и компоненты перемещений ![]() во внутренних
границах и внешнем контуре цилиндра совпадают с решениями МГЭ точностью до 10-4.
во внутренних
границах и внешнем контуре цилиндра совпадают с решениями МГЭ точностью до 10-4.
Литература
1. Иманбаева Л.Х., Канатов А.С., Метод криволинейных
сеток в треугольных элементах //Тезисы докладов 10-ой Межвузовской конференции
по математике и механике/ЭВЕРО. Алматы, 2004. С. 129.
2. Жадрасинов Н.Т. Нелинейная деформация составных
оболочек. Алматы: Ғылым, 1998. 174 с.
3. П. Бенерджи, Р.
Баттерфилд Методы граничных элементов в прикладных науках. М.: Мир, 1984. 494с.