Карачун В.В., Мельник В.Н.

Национальный технический университет Украины «КПИ»

Стационарная задача ВОЗДЕЙСТВИЯ ПЛОСКОЙ ВОЛНЫ НА ПЛАСТИНУ С ЗАКРЕПЛЕННЫМ ЦЕНТРОМ

Выкладки сделаем в общей постановке, для внешнего возмущающего воздействия любой структуры.

Пусть на пластину действует стационарная плоская звуковая волна вида

,

где – постоянные коэффициенты; – волновое число; – цилиндрическая жесткость пластины; – амплитуда звукового давления.

Обозначим : ; ; ; .

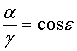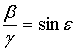Тогда –

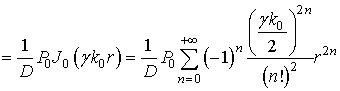(1)

и

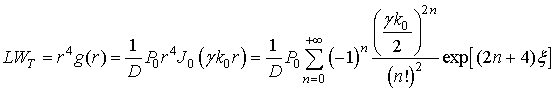, (2)

где .

Найдем частное решение уравнения (2) в виде суммы степенного ряда относительно

(3)

с коэффициентами , подлежащими определению.

Подстановка (3) в уравнение

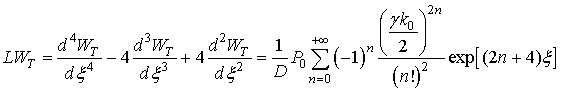(4.85)

дает:

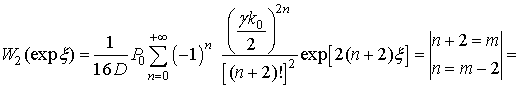
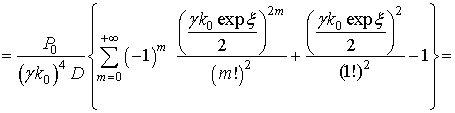
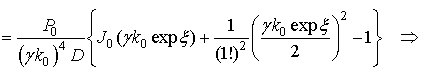
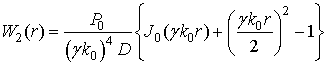(5)

Таким образом, решения уравнения движения для этого случая имеет вид:

. (6)

Разумеется, слагаемое 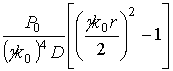можно было бы опустить, так как оно является частным решением однородного уравнения , и взять частное решение неоднородного уравнения (2) в такой форме –

. (7)

Несмотря на то, что , все же

.

Таким образом, для плоской волны акустического воздействия предельное решение строится в соответствии с формулой, в которой значение определяется соотношением (5):

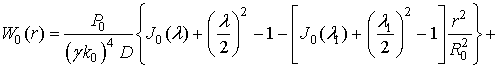
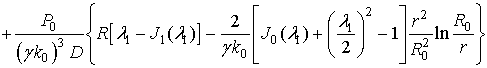, (8)

где – безразмерная переменная; – безразмерная константа; – безразмерная константа; .