Бондаренко Л. М., Проскурня В. Н., Азімов Р. Р.

Дніпропетровський національний університет залізничного транспорту імені Академіка В. Лазаряна

УТОЧНЕНИЯ К РАСЧЕТУ ЛЕНТОЧНО-КОЛОДОЧНЫХ ТОРМОЗОВ

Ленточно-колодочные тормоза применяют в машинах с режимом работы (экскаваторы, лебедки бурового оборудования, шахтные подъемные машины и т.п.). В этих тормозах накладки изготовляют в виде отдельных жестких колодок, прикрепленных к относительно гибкой стальной ленте, которую можно считать не деформируемой.

В справочной литературе и диссертациях приводятся, по крайней мере, три формулы, дающие существенно различные величины отношений натяжений набегающей и сбегающей ветвей ленты при реальном числе накладок. Учитывая ответственность тормозов, необходимо дать анализ существующих формул и предложить более точную.

В [1], при жестком креплении колодок, отклонение натяжения в набегающей ветви Т_нб к натяжению в сбегающей Т_сб рекомендуется определять по следующей формуле:

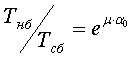, (1)
где - угол обхвата лентой шкива, измеряемый между линиями, соединяющими центры крайних колодок с центром шкива; n – количество колодок; - полный угол обхвата.

В [2] эта формула имеет вид

, (2)
где b - угол между осями смежных колодок (при одинаковой длине колодок равен центральному углу, образуемого колодкой).

В [3] это отношение записано в виде:

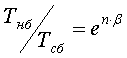. (3)

Очевидно, что формулы (1) и (3) предполагают колодку абсолютно гибкой, что в конечном результате приводит к формуле Эйлера (3).

Отношения , получение по формулам (1), (2), (3) при a = 270º; m = 0,4 и процентные расхождения с (3) в зависимости от числа накладок приведены в таблице 1.

Таблица 1

n	(1)	%%	(2)	%%	(3)
5	4,52	31,4	5,53	16,0	6,58
10	5,45	17,3	5,79	12,0
15	5,81	11,8	5,98	9,1
20	5,99	9,1	6,11	7,2

Цель исследования: установить отношение натяжения в набегающей ветви к его величине в сбегающей, с учетом, что колодка абсолютно жесткая на изгиб.

Представим одну колодку в виде, показанном на рис.1.

Сила прижатия колодки, приведенная к ее середине, составит

.

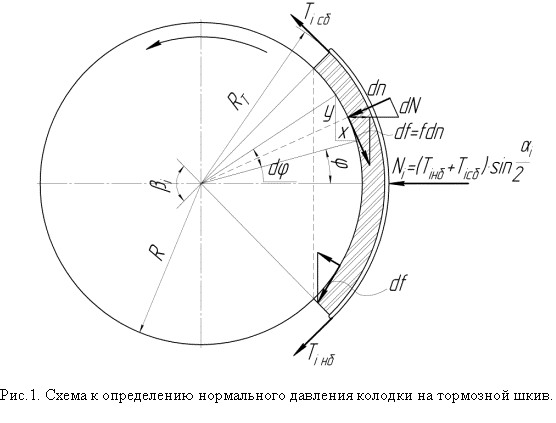
Для нахождения закона распределения нормальных усилий по высоте колодки найдем распределение давления на катет у (игрек) элементарного сектора с углом

, (4)

Поскольку

, (5)
то давление на этот катет

. (6)

Интеграл выражения (5) в пределах угла обхвата b_i дает полную величину нормального давления колодки на тормозной шкив

. (7)

Таким образом, при известной силе в точке сбегания сила нормального давления i-той колодки на шкив составит

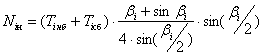, (8)
а усилие в точке набегания составит

(9)
или

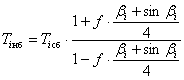. (10)

При условии, что и при равенстве углов обхвата каждой колодкой шкива равным b, числе колодок n, получим

. (11)

Отношения , полученным по формуле (11) приведены в таблице 2.

Таблица 2

n	(11)	%%
5	5,87	10,8
10	6,40	2,7
15	6,50	1,2
20	6,54	0,7

Отметим, что расхождения с (3) приведены чисто условно.

Анализ полученных формул и результатов вычислений отношений позволяет сделать такие выводы и предложения:

- формулы (1), (2) и (11) дают одинаковые отношения при числе колодок n ³ 50;

- формула (11), полученная из условия абсолютной жесткости колодки на изгиб наиболее точно отвечает постановке задачи;

- при расчете ленточно–колодочных тормозов необходимо пользоваться формулой (11).

ЛИТЕРАТУРА

1. Тормозные устройства: Справочник/Александров М. П., Лысяков А. Г., Федосеев В. Н. и др. – М.: Машиностроение, 1985. – 312 с.

2. Справочник по кранам: В 2 т. Т.2/Александров М. П., Гохберг М. М., Ковин А. А. и др. – Л.: Машиностроение, 1988. – 599с.

3. Криштопа Л. І. Навантаженість багатопарних фрикційних вузлів гальмівних систем бурових лебідок. // Автореферат дисертації. Канд. техн. наук. Івано-Франківськ.