Математика

1. Дифференциальные и интегральные уравнения

Шилинец В. А., Пташинская О. И.

Белорусский государственный педагогический университет

ИССЛЕДОВАНИЕ ФУНКЦИОНАЛЬНО-ИНВАРИАНТНЫХ РЕШЕНИЙ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ МАКСВЕЛЛА ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ В ПУСТОТЕ

В ряде работ [1-3] изучались так называемые функционально-инвариантные решения системы дифференциальных уравнений Максвелла для электромагнитного поля в пустоте

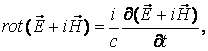(1)

где − вектор электрической напряженности поля, − вектор магнитной напряженности поля, − скорость света в пустоте.

В работе [3] была поставлена и решена задача об интегральном представлении некоторых видов решений системы уравнений Максвелла. Целью данного исследования является получение интегрального представления Фёдорова для новых видов решений системы (1), какие не рассматривались в работе [3], а также решение краевой задачи для системы (1).

Приведём необходимые для дальнейшего определения.

Определение 1. Если вектор , где − скалярные комплексные функции от , является решением системы (1), то решением этой системы будем называть и гиперкомплексную функцию ,

где .

Определение 2. Гиперкомплексная функция

называется моногенной в смысле

В.С. Фёдорова (F-моногенной) [4] по другой гиперкомплексной функции в некоторой односвязной области действительного евклидова пространства , если найдётся такая третья функция от , что для любой фиксированной точки и любой переменной точки имеем , где (аналогично для ), .

Определение 3. Решение системы (1) называется функционально-инвариантным, если любая функция, F-моногенная по , например, аналитическая от , также является решением системы (1).

В работе [1] показано, линейная от , , , функция

(2)

является функционально-инвариантным решением системы (1), если , − произвольные константы, а

, ,

, , (3)

где , , .

Задача. Найти интегральное представление Фёдорова для F-моногенных по функций, которые, как известно (определение 3), являются решениями системы (1) и при этом отличаются от функций − решений системы (1), для которых интегральное представление Фёдорова построено в статье [3].

Решение. Как известно [5], для любой функции , F-моногенной по в области , имеет место интегральное представление

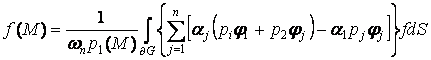, (4)

если функция удовлетворяет в области условиям

, , (Ф)

где , , , , , , , , 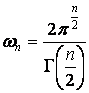, под знаком интеграла , − направляющие косинусы внешней нормали к , , , .

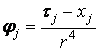
Представление (4) в дальнейшем будем называть представлением Фёдорова, а условия (Ф) − условиями Фёдорова.

Легко проверить, что функционально-инвариантное решение системы (1) − функция , определяемая формулой (2) при , , , , удовлетворяет условиям Фёдорова (Ф). Необходимо отметить, что получено новое функционально-инвариантное решение системы Максвелла (1), которое не было получено в работе [3] и которое удовлетворяет условиям Фёдорова (Ф).

Таким образом, для любой функции , F-моногенной по функции в области , являющейся как и функция решением системы Максвелла (1), получим

где , определяются по формулам (3) при условии, что , , ,.

Задача решена. Получено интегральное представление Фёдорова для нового класса решений системы Максвелла (1).

Замечание. Полученное интегральное представление позволяет решить следующую краевую задачу.

Задача. Пусть функция , определяемая формулой (2) при , , , , и функция , моногенная в смысле В. С. Фёдорова по функции , определены на некоторой замкнутой трёхмерной поверхности , гомеоморфной сфере конечного диаметра и достаточно гладкой для возможности использовать формулу Остроградского ( − внутренность поверхности ).

Требуется найти в любой точке значение функции , моногенной в смысле В. С. Фёдорова по , если известны её значения на поверхности .

Литература

1. Стельмашук Н.Т. Об одном исследовании системы Максвелла с помощью F-моногенных функций // Журнал вычислительной математики и математической физики. − 1967. − Т.7,№2. − С.431-436.

2. Стельмашук Н.Т. Решение некоторых систем дифференциальных уравнений в частных производных // Дифференциальные уравнения. − 1977. − Т.12,№8. − С.1427-1433.

3. Стэльмашук М.Т., Шылінец У.А. Аб адной краявой задачы для функцыянальна-інварыянтных рашэнняў сістэмы Максвэла // Весці БДПУ. − 1994. − №1. − С.91-95.

4. Федоров В.С. Основные свойства обобщенных моногенных функций // Известия вузов. Математика. − 1958. − №6. − С.257-265.

5. Федоров В.С. Об одном обобщении интеграла типа Коши в пространстве // Известия вузов. Математика. − 1957. − №1. − С.227-231.