Шилинец В.А., Берегейко Е.И., Ольшевская А.В.

Белорусский государственный педагогический университет

ИССЛЕДОВАНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ОДНОГО КЛАССА ФУНКЦИОНАЛЬНО-ИНВАРИАНТНЫХ ВЕКТОР-АНАЛИТИЧЕСКИХ ФУНКЦИЙ

Функционально-инвариантные решения некоторых уравнений математической физики изучались многими авторами [1-6].

Как известно [1-4], функционально-инвариантным решением уравнения

называется такое решение , если произвольная дважды дифференцируемая функция также является решением этого уравнения.

Цель нашей статьи − решение краевой задачи для одного класса функционально-инвариантных вектор-аналитических функций.

Нам требуются некоторые определения.

Определение 1. Следуя Рейниху, называем вектор-функцию ( − комплекснозначные дважды непрерывно дифференцируемые функции от координат в некоторой области ) вектор-аналитеческой [5-7], если

,. (1)

Если вектор-аналитической является вектор-функция , то вектор-аналитической будем называть и гиперкомплексную функцию , где − база какой-либо линейной ассоциативно-коммутативной алгебры с единицей над полем комплексных чисел.

Система (1) является некоторым обобщением известной системы Коши-Римана на трехмерное пространство и частным стационарным случаем системы Максвелла для электромагнитного поля в пустоте , , , , если положить в этой системе , где и т. п.

Определение 2. Гиперкомплексная функция

называется моногенной в смысле В.С. Федорова (- моногенной) [8] по другой гиперкомплексной функции в некоторой области , если найдется такая функция , что для всех точек области имеем

, (2)

где ; , , .

Определение 3. Вектор-аналитическая функция называется функционально-инвариантной, если всякая функция , моногенная в смысле В.С. Федорова по , будучи записана в виде , также определяет вектор-аналитическую функцию , т.е. , .

В настоящей работе мы ограничимся случаем такой алгебры , в которой , , , причем .

В работе [9] в случае алгебры доказана теорема.

Теорема 1. Вектор-аналитическая функция будет функционально-инвариантным решением системы (1), если компоненты удовлетворяют следующей системе:

, (3)

, , (4)

, . (5)

Рассмотрим следующую краевую задачу.

Задача. Пусть − линейное относительно , , функционально-инвариантное решение системы (1), т.е.

,

, , ,

удовлетворяют системе (3) - (5).

Полагаем далее, что и функция , - моногенная по , определены на некоторой замкнутой двумерной поверхности , гомеоморфной сфере конечного диаметра и достаточно гладкой для возможности использовать формулу Остроградского ( − внутренность поверхности ).

Требуется найти в любой точке значение функции , моногенной в смысле В. С. Федорова по , если известны ее значения на поверхности .

Для решения сформулированной задачи используем следующее представление В.С. Федорова [10]: если

1) функция − моногенная в смысле В.С. Федорова по в области ;

2) , , , (Ф)

то для каждой точки имеем

, (6)

где под знаком интеграла , точка , − направляющие косинусы внешней нормали к ,

, , .

Чтобы использовать формулу (6) для решения сформулированной задачи, необходимо найти линейную функционально-инвариантную вектор-аналитическую функцию, удовлетворяющую условиям (Ф), т.е. условиям

В. С. Федорова.

Имеем , . Функцию определим из равенства (3). Подставив в (4) и (5), получим систему

, ,

, .

Считая произвольными константами, находим

, , ,

причем удовлетворяют условию

.

Таким образом, получаем

,

,

, .

можно задавать произвольно, требуя только выполнение условия

.

Пусть , , ,

тогда

,

.

Таким образом, получили функционально-инвариантную вектор-аналитическую функцию

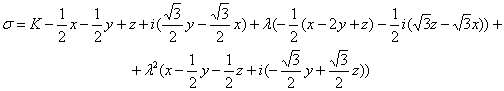, (7)

и функционально-инвариантными вектор-аналитическими окажутся, например, функции , в силу их - моногенности по .

Легко проверить, что функционально-инвариантная вектор-аналитическая функция (7) удовлетворяет условиям Федорова (Ф), и для функции , моногенной по , имеет место интегральное представление (6), при помощи которого и решается сформулированная выше краевая задача.

Литература

1. Соболев С.Л. Функционально-инвариантные решения волнового уравнения // Тр. физ.-мат. ин-та АН СССР, 1934. − Вып.5. − С. 117-128.

2. Смирнов В.И. Курс высшей математики. −М., 1957. − Т. 3. − Ч. 2. − С. 196-204.

3. Еругин Н.П. Функционально-инвариантные решения уравнений гиперболического типа с двумя неизвестными переменными // Уч. зап. ЛГУ. Сер. мат. наук, 1949. − Вып. 16. − С. 142-166.

4. Смирнов М.М. Функционально-инвариантные решения волнового уравнения // Докл. АН СССР, 1949. − Т. 67. − №6. − С. 977-980.

5. Стельмашук Н.Т., Шилинец В.А. Об интегральном представлении функционально-инвариантных вектор-аналитических функций // Весці НАН Беларусі. Сер. фіз.-мат. навук, 2006. − №1. − С. 44-47.

6. Стэльмашук М.Т., Шылінец У.А. Аб адной краявой задачы для функцыянальна-інварыянтных вектар-аналітычных функцый // Весці БДПУ, 1995. − №1. − С.85-88.

7. Reinich G.Y. Analitic functions and math. physics // Bull. Amer. Math. Soc., 1931. − Vol. 37. − P. 689-714.

8. Федоров В.С. Основные свойства обобщенных моногенных функций // Изв. вузов. Математика, 1958. − №6. − С. 257-265.

9. Стельмашук Н.Т. О вектор-аналитических функционально-инвариантных функциях // Тез. докл. итоговой науч.-техн. конф. Ивановского энергетического ин-та им. В.И. Ленина, 1967. − С. 35.

10. Федоров В.С. Об одном обобщении интеграла типа Коши в многомерном пространстве // Изв. вузов. Математика, 1957. − №1. − С. 227-233.