К.т.н. Иванов Д.В., д.т.н. Ангилеев О.Г.

ФГБОУ ВПО Ставропольский государственный аграрный университет

Модель динамики энергосодержания растительных кормовых материалов

Теоретическая основа модели базируется на общем законе сохранения энергии и положении, что все процессы в природе, связанные с превращением энергии, находятся в строго определенных количественных соотношениях.

Биоцикл развития растений и биохимические превращения, происходящие в процессе хранения, представляют собой непрерывную цепь накопления и потери энергии содержащейся в продукте.

Модель динамики энергосодержания кормов состоит из трех элементов – динамики энергонасыщения корма (Э_о), происходящее вследствие природных факторов и выполнения должных агротехнологических операций, динамики постепенного или ступенчатого снижения энергосодержания корма (рассеивания его потенциальной энергии) (Э_рас.) под воздействием неблагоприятных внешних факторов и биохимических процессов, и их разности представленной остаточной энергией корма (Э).

Характеристикой названных элементов являются удельные показатели продукта выраженные в МДж.

Энергия корма (Э) в текущий момент времени (t) определяется из уравнения баланса энергии [1] как , (1)

где Э - остаточная обменная энергия корма в момент времени t, МДж; Э_о -энергия полученная растительным материалом на i-тых этапах роста, МДж; Э_рас. - энергия, рассеянная в процессе преобразования растения, обработки и хранения корма, МДж.

Из уравнения рассеяния энергии [1] известно , (2)

где Т - абсолютная температура, К; S - энтропия, МДж/К;

Тогда уравнение (1) примет вид . (3)

Для рассмотрения его использован известный метод анализа размерностей используемый как способ исследования неявных переменных в сложных системах [2].

Энергия полученная растительным материалом на i-ом этапе (Э_оi) и сопутствующая ей энтропия (S_i) могут быть представлены табличными формулами размерностей, как

(4) и , (5)

где М - масса, т; L - расстояние, м; Θ - время, ч; Т - температура, К.

Подставив формулы (4) и (5) в уравнение (3), получим

, (6)

где и

Выражение (6), отражая картину в целом, не учитывает востребованной части энергии, не учитывает затрат механической энергии на уборку, транспортировку и придание кормовым материалам состояния пригодного для хранения, не предусматривает мероприятий направленных на снижение энтропии. Для устранения названного выполнены следующие преобразования.

Поскольку в общей энергии корма (Э) потребительский интерес вызывает лишь обменная энергия [ОЭ], представляющая собой «… часть энергии корма, которая может быть продуктивно использована в пищеварительном процессе данного вида животных» [3], энергию корма можно представить равенством

(7а) или (7б)

Чтобы обеспечить сохранность обменной энергии кормовой материал подвергают многооперационному воздействию с затратой мощности (N) (механической энергии), описываемой табличной формулой преобразования размерностей [2]: (8)

Тогда формула (4) преобразуется в выражение

(9)

Энтропия, после придания корму состояния пригодного для длительного хранения, соответственно снизится на некоторую величину

(10)

Соотношение обменной энергии корма [ОЭ] с энтропией (S) составит:

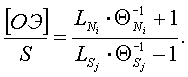(11)

Энтропия, как мера обесценивания энергии, может быть рассмотрена также в виде функции термодинамической системы, отражающей тепловое состояние корма во время уплотнения и хранения его.

Зная табличное значение размерности коэффициента теплопроводности

равное (12)

вычислим значение М как (13)

Подставив выражение (13) в формулу (5) и проведя соответствующие сокращения определим величину термодинамической энтропии

(14)

где основным фактором, определяющем энтропию тепловой энергии вследствие самонагревания растительной резки, является коэффициент теплопроводности материала (k).

Предложенная модель позволяет вести исследование неявных переменных в сложной системе накопления и энтропии обменной энергии корма, принимать научно-обоснованные решения по выбору и совершенствованию технологии переработки кормов, подготовки их к длительному хранению и эффективному использованию.

ЛИТЕРАТУРА

1. Хендель А. Основные законы физики. Пер. с нем. – М.: Госиздат физ.-мат. литературы, 1959. – С. 285.

2. Шенк Х. Теория инженерного эксперимента. Пер. с англ. – М.: «Мир», 1972. – С. 382.

3. Олдмит Т. Технология приготовления силоса и кормление коров в Голландии. Пер. с англ. – М., 1969. – С. 128.