Доповідь/Технічні науки – Автоматизовані системи управління на виробництві

УДК 681.5.015

Семенцов Г.Н., Сабат Н.В., Чигур Л.Я.

Івано-Франківський національний технічний університет нафти і газу

МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ БУРИМОСТІ ГІРСЬКИХ

Роботу присвячено розробленню математичної моделі буримості гірських порід, інформація про яку є необхідною передумовою вибору раціонального типу бурового долота і оптимізації процесу буріння нафтових і газових свердловин.

Розглянуто особливості кількісних мір оцінювання буримості гірських порід (початкової механічної швидкості буріння ν₀; тривалості буріння фіксованого значення проходки t_ф; величини проходки за фіксований час h_ф; енергоємності буріння одиниці ствола Е; питомої енергії руйнування породи Е_п ) і взаємозв’язків її з абразивністю порід.

Показано, що лише для доліт, знос озброєння яких для певних інтервалів глибин незначний, оцінювати буримість можна за механічною швидкістю буріння:

, (1)

де φ(t) – функція зносу долота.

Для опису зміни механічної швидкості буріння запропоновано використати залежність

, (2)

де К_v – коефіцієнт, який характеризує інтенсивність зношення долота і залежить від абразивних властивостей породи; т – ціле додатне число, яке належить множині N: N = {0,1,2,3}.

Отримано рівняння

, (3)

яке дало змогу визначити функцію зносу долота φ(t) при різних значеннях т і при початковій умові φ(0)=1.

Показано, що оцінкою буримості гірської породи може слугувати початкова швидкість буріння ν₀ за умови, що відомі певні базові режимні параметри.

Запропоновано розглядати сукупність «долото – порода» як єдиний об’єкт контролю (рис.1), стан якого характеризується параметрами стану долота де t – поточний час основного періоду роботи долота; - оцінки зносу озброєння і опор долота, а також оцінкою міцності гірських порід, якою обрали такий показник як буримість порід f.

Рис.1. Структурна схема процесу буріння свердловин як об’єкта контролю буримості в просторових координатах: - контрольовані параметри

З множини зовнішніх впливів, які діють на об’єкт контролю, вибрані лише ті, що суттєво впливають на ефективність руйнування породи: вхідні керувальні дії

= [F(t), n(t), Q(t)] (4)

і апріорі відомі параметри долота

де F – осьова сила на долото; n – швидкість обертання долота; Q(t) – витрата промивного розчину; d – діаметр долота; n_ш – кількість шарошок; n_з – кількість зубців на шарошках.

Показано, що параметри стану долота Z(t) пов’язані з вхідними керувальними впливами X(t), параметрами долота і буримістю порід f залежністю Z_і(t) = B_i [(t), α_i, f], і = 1,2…,k, де і – кількість доліт.

Вплив стану об’єкта контролю на показники процесу буріння запропоновано характеризувати значеннями його вихідних величин : проходки долота h(t) і механічної швидкості буріння υ(t), тобто Кожна з вихідних величин визначається через параметри стану Z(t) своєю функціональною залежністю j = 1,2. Параметри контролю визначаються через вхідні і вихідні величини об’єкта l = 1,…,4.

Визначено клас задачі контролю буримості гірських порід як виявлення подій в умовах невизначеності і показник буримості запропоновано визначати безконтактним методом на базі комплексу контрольованих параметрів

f = М(,). (5)

При незмінному векторі керувальних дій побудовано узагальнену математичну модель початкової механічної швидкості

, (6)

де Б(t), А(t) – параметри, що характеризують буримість і абразивність породи.

Після введення додаткових умов використання математичної моделі, що містять тип оснащення долота і обмеження на мінімально допустиму витрату промивальної рідини Q, встановлено, що вихідна функція v₀ залежить від F, n, d і потужності Р на долоті. Показано, що між всіма цими параметрами існує деяка функціональна залежність φ(v₀, F, n, P, d)=0, для розкриття якої перейшли від початкових розмірних координат до безрозмірних змінних, і скориставшись π-теоремою Букінгема, одержали одну безрозмірну комбінацію, від якої залежить остаточний розв’язок задачі:

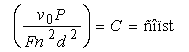, (7)

де v₀, F, n, P, d – числові значення відповідних величин при деякому вибраному наборі основних одиниць фізичних величин.

З врахуванням виразу для потужності на долоті, де C_p – коефіцієнт, який враховує розмірність потужності, - невідомі показники степеня, що підлягають ідентифікації, отримали узагальнену математичну модель

. (8)

Запропоновано для визначення постійних складових у величинах F, n ввести до розгляду базові величини n₀, F₀: n(t)= n₀ + (t), F(t)=F₀+(t), де (t), (t) – стаціонарні в межах рейсу долота ергодичні випадкові процеси з нульовим математичним сподіванням.

Тоді узагальнена математична модель (8) набула такого вигляду

, (9)

де k = C_pD²; α = 1-γ; β = 2-δ.

Розглянуто задачу оцінки впливу зносу озброєння традиційного шарошкового долота на механічну швидкість буріння.

Показано, що, якщо врахувати значення φ(t), то можна визначити величини ε_y , dφ/dt, dε_y /dt (табл. 1). На основі аналізу показників зношення доліт зроблено висновок, що, якщо механічна швидкість буріння змінюється за гіперболічним законом, тобто φ(t) = 1+К_εt, тоді за показником можна оцінювати абразивність гірських порід.

Величину позначили як .

Висунута гіпотеза і сформульовані допущення дали змогу в результаті аналізу математичних моделей встановити, що під час буріння в однорідному за буримістю інтервалі гірських порід, коли керувальні впливи F = const, n = const, буримість гірських порід можна оцінити опосередкованою функцією 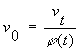, φ(t) – функція, яка характеризує знос озброєння долота. Ця функція, залежить від типу вибраної моделі.

Запропоновано як базове значення механічної швидкості буріння обрати ту механічну швидкість, яка визначається на початку буріння алмазним долотом або незатупленим шарошковим долотом з оптимальними керувальними діями.

Висновок

На основі результатів досліджень взаємозв’язків основних факторів, що визначають буримість гірської породи, обгрунтовано найбільш інформативний параметр для оцінювання буримості породи в реальному часі, розроблено узагальнену математичну модель буримості в просторі станів, а також динамічну інформаційну модель і метод визначення базових значень показника буримості, який полягає у тому, що для автоматизованого безконтактного контролю буримості гірських порід обирається та механічна швидкість, яка визначається на початку буріння алмазним або незатупленим шарошковим долотом при бурінні з оптимальними параметрами режиму, що дає змогу визначати зв’язки показників буримості з глибиною свердловини, які є базою для поточної оптимізації та вибору оптимальних режимів під час проектування режимів буріння інших свердловин, що буряться в аналогічних умовах.

Література:

1. Семенцов Г.Н. Концептуальна математична модель процесу буріння нафтових і газових свердловин долотами нового покоління як об‘єкта контролю і керування / Г.Н.Семенцов, Л.Я.Чигур // Вісник Хмельницького національного університету. - 2010. - С.72-79.

2. Семенцов Г.Н. Визначення буримості гірських порід шляхом вимірювання параметрів і показників процесу буріння / Г.Н.Семенцов, Н.В.Сабат // Науковий вісник Хмельницького національного університету,№1. - 2007. - С.181-186.

3. КогучЯ.Р. Вимоги до математичної моделі буримості гірських порід з позицій автоматичного контролю / Я.Р.Когуч, Н.В. Сабат // Науковий вісник: ІФНТУНГ. - 2004. - С.49-53.

4. Сабат Н.В. Метод контролю буримості гірських порід в процесі поглиблення свердловин / Н.В.Сабат // Академический вестник, Кривой Рог, № 19. - 2007. - С.52-53.