Ст.к. Хамаева А.Р., к.т.н. Кузнецова С.Г.
Пермский
национальный исследовательский политехнический университет, Россия
Определение эффективной
оси в трехшарнирной системе.
Разное
очертание арки предполагает разное
напряжённое состояние элементов конструкции. Для выявления наиболее
рационального очертания оси трехшарнирной арки, при которой на элементы
конструкции затрачивается меньше усилий, рассмотрим трехшарнирную арку,
изображенную на рис.1, при заданной нагрузке и положении шарнира.
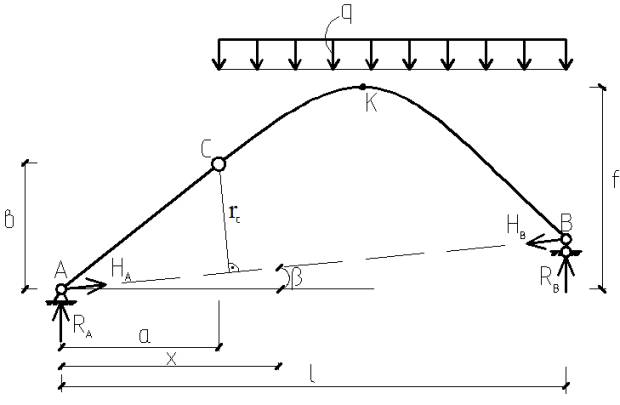
Рис.1 Трехшарнирная арка.
Найдем реакции на опорах RА, RB и распоры HA и HВ:
ΣМА=0,
q(![]() -a)
-a)![]() (
(![]() )-RB
)-RB![]() =0; RB=
=0; RB=![]() ;
;
ΣМB=0, -![]() +RA
+RA![]() =0; RА=
=0; RА=![]() ;
;
Σ =0, RA
=0, RA![]() a-HA
a-HA![]() rC=0 (
rC=0 (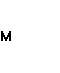 -HA
-HA![]() rC=0);
rC=0);
где 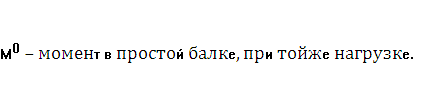
Σ![]() =0, HA
= HВ= H; RB=
=0, HA
= HВ= H; RB=![]() ;
;
rC=cosβ(b-a![]() tgβ);
tgβ);
Из
трех последних выражений выразим распор Н:
Н =
=
Запишем
уравнение для прямолинейного отрезка оси арки А-С: у = k![]() x=
x=![]() x.
x.
Для того чтобы определить какое рациональное очертание
имеет криволинейный отрезок оси арки, найдем его уравнение.
Выразим момент в любой точке для криволинейного отрезка
арки, изображенного на рис.1:
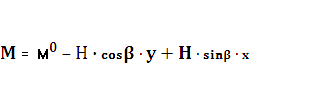 ,
,
Рациональная ось арки определяется из равенства: ![]() ,
,
т.е. 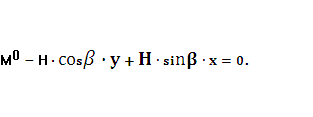 Отсюда получим:
Отсюда получим:
.
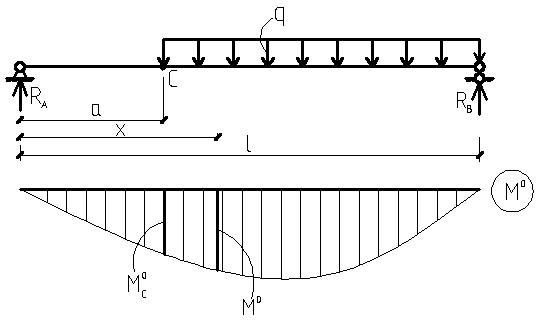
Рис.2 Простая балка, соответствующая арке,
изображенной на рис.1.
Момент в сечении С, изображенный на рис.2, равен:
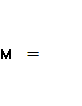 RА
RА![]() а.
а.
Момент в произвольном сечении для криволинейного отрезка
этой же балки, изображенного на рис.2:
 RА
RА![]() х -
х - ![]() .
.
Подставив
все известные нам выражения в уравнение (1), получим:
у=х![]() tgβ+(b-a
tgβ+(b-a![]() tgβ)
tgβ)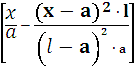 (2).
(2).
Определим координаты вершины. Для того чтобы найти
абсциссу вершины, найдем первую производную ![]() и приравняем ее к нулю:
и приравняем ее к нулю:
у’=tgβ+![]() ,
,
tgβ+![]() .
.
Из последнего уравнения выразим абсциссу вершины ![]() :
:

Подставим ![]() (2) и найдем значение ординаты в вершине арки:
(2) и найдем значение ординаты в вершине арки:
Из уравнения (2) очевидно, что
вторая степень абсциссы наибольшая. Таким образом, рациональной осью арки
является парабола с координатами вершины (![]() ).
).
Литература:
1.
Дарков А.В., Шапашников
Н.Н. Строительная механика: Учебник. 9-е изд., испр.-СПб.: Издательство
«Лань»,2004. 656 с.: ил. – (Учебники для вузов. Специальная литература).
2.
Руководство к
практическим занятиям по курсу строительной механики, под общей редакцией д-ра
техн. Наук. Проф. Г.К. Клейна.