Педагогические науки/1. Дистанционное образование

Флегантов Л. О.

Полтавська державна аграрна академія, Україна

Cамостійна робота студентів з використанням системи WolframAlpha при навчанні математичних дисциплін у web-зорієнтованій методичній системі навчання

Одне з головних завдань процесу навчання у ВНЗ – навчити студентів працювати і поповнювати свої знання самостійно. Самостійна робота сприяє розвитку творчого мислення та індивідуальних здібностей студентів у розв’язанні теоретичних та практичних завдань, прищепленню студентам навичок самостійної науково-дослідницької діяльності, залученню їх до розв’язання наукових проблем, поглибленню знань у певному науковому напрямі, формуванню вмінь виконання розрахунково-графічних, курсових та дипломних робіт, дипломних проектів тощо. Самостійна та індивідуальна робота студентів служить пропедевтиці подальшої науково-дослідницької діяльності студентів, магістрів та аспірантів у вищій школі.

Web-зорієнтована методична система навчання – різновид інформаційної системи навчання. Термін «web-орієнтована» означає, що головним технічним інформаційним засобом навчання є сукупність web-сервісів та web-технологій. Web-зорієнтоване навчання може бути реалізоване у будь-якій існуючій методичній системі – від репродуктивного, догматичного до проективного, з усіма властивими методичній системі функціями.

В основі самостійної роботи студентів лежить поняття самостійності, яке означає здатність людини виконувати певні цілеспрямовані дії або цілісний комплекс цілеспрямованих дій без допомоги з боку іншої людини або технічних засобів, що її замінюють, керуючись лише власним досвідом. Ця здатність лежить в основі самостійної діяльності людини.

Традиційні форми СРС – домашні завдання, опрацювання інформаційних (зокрема, літературних) джерел, робота у комп’ютерних мережах, складання анотацій навчальних модулів, оцінювання ситуацій у галузі професійного спрямування, підготовка конспекту лекцій, практичних занять, звітів про виконання лабораторних робіт, виконання розрахунково-графічних, курсових робіт, робота над окремими частинами дипломних робіт і проектів.

Розв’язування задач є важливим елементом самостійної роботи студентів з математичних дисциплін. Самостійне вивчення теоретичного матеріалу, читання підручника, повинно обов’язково супроводжуватися розв’язуванням задач. Розв’язування задач, які відносяться до розділу курсу, що вивчається, треба розпочинати з розбору прикладів розв’язаних задач у підручнику і на практичних заняттях, і лише потім переходити до розв’язування задач, запропонованих для самостійної роботи.

Якщо в процесі самостійної роботи над вивченням теоретичного матеріалу або при розв’язуванні математичних задач студент зіткнувся з труднощами, розв’язати самостійно які йому не вдалося, то йому слід обов’язково звернутися за консультацією. Питання, що виникають, можуть стосуватися, зокрема, незрозумілих термінів, формулювань означень і теорем, окремих задач тощо. У web-зорієнтованій методичній системі навчання студент має набагато більше можливостей одержати консультацію: він може скористатися пошуком інформації в Інтернет, надіслати своє питання, як коментар до відповідного розділу у блозі навчальної дисципліни, задати його на форумі навчальної дисципліни, звернутися за консультацією до викладача особисто, елктронною поштою, у чаті або під час проведення тематичного вебінару, тощо. При цьому викладач має наполягати, щоб у своїх питаннях кожен студент точно вказував, в чому конкретно він має труднощі. Якщо він не розібрався в теоретичних положеннях, то має чітко вказати на опрацьоване ним джерело (наприклад, указати назву, автора підручника, рік видання і сторінку). Якщо студент має труднощі при розв’язуванні конкретної задачі, то йому слід описати характер цих труднощів і навести свій варіант або принаймні приблизний план розв’язання задачі.

Розглянемо СРС з вивчення основ математичного аналізу на основі використання онлайнового процесору знань WolframAlpha.

Стандартним завданням СРС з основ математичного аналізу є практика обчислення границь виду , дета - многочлени степеня . Висновок про те, як у випадку невизначеності типу можна швидко обчислювати такі границі не вдаючись до стандартних, іноді досить громіздких і витратних за часом перетворень, студенти зазвичай формулюють після розв’язання великої кількості однотипних прикладів під керівництвом викладача, або після його прямої вказівки.

За допомогою web-сервісу WolframAlpha студенти здатні самостійно сформулювати потрібний висновок. Необхідно лише сформулювати студентові відповідне завдання і забезпечити методичими вказівками для самостійної роботи.

Перед виконанням розрахунково-графічних завдань і типових розрахунків з математичних дисциплін студенти попередньо мають ознайомитися з процедурою та прикладами використання системи WolframAlpha за допомогою методичних вказівок до СРС, розміщених у блозі викладача (wolframalpha-ru.blogspot.com).

Розглянемо процедуру обчислення границь за допомогою онлайнового процесора WolframAlpha. Нехай необхідно обчислити границю: . Спроба обчислення таких границь приводить до невизначеності типу .

Система WolframAlpha практично миттєво виводить розв’язок такої вправи. Для цього слід скористатися пошуковим запитом виду:

lim (2x^3-3x+10)/(3x3-2x^2+4x-5) x -> +infinity

У відповідь на цей запит WolframAlpha виводить web-сторінку з інформацією у наступному вигляді (Рис. 1).

Якщо студентові необхідно одержати консультацію з приводу розв’язку цього прикладу звичайним способом, WolframAlpha надає йому цю можливість. Для цього слід скористатися послугою “Show steps” (Показати кроки). Система WolframAlpha для обчислення даної границі послідовно тричі застосовує правило Лопіталя.

Рис. 1. Результат обчислення границі у системі WolframAlpha.

За невеликий проміжок часу, використовуючи послуги системи WolframAlpha, студент може самостйно одержати і проаналізувати розв’язки великої кількості однотипних прикладів. Це надасть йому необхідний фактичний матеріал, і створить передумови для самостійного «виведення» правила швидкого розкриття невизначенностей типу . Це буде, фактично, емпіричний умовивід, який неявно використовує метод математичної індукції.

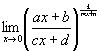Аналогічним чином можна надати студентам можливість самостійно сформулювати більш складне правило обчислення границь, що приводять до невизначенності типу . Наприклад, навіть для таких, як тощо.

Помітним результатом систематичного застосування web-сервісу WolframAlpha у СРС при вивченны математичних дисциплын є підвищення зацікавленості, самооцінки студентів, їх впевненості у собі, покращення загальної успішності. Використання WolframAlpha та інших соціальних web-сервісів з метою ефективної організації СРС є перспективним напрямком і важливим завданням подальших досліджень.