Педагогические науки/ 5.Современные методы преподавания

Михин М.Н. Пяткин В.В.

Московский государственный университет приборостроения и информатики

Применение производной в геометрии при нахождении расстояния от точки до пространственной прямой

Пусть требуется найти расстояние от точки до прямой в пространстве. Расстоянием от точки до прямой, не проходящей через заданную точку, называется длина перпендикуляра, опущенного из данной точки на заданную прямую. Как правило, для нахождения расстояния от точки до прямой находят проекцию этой точки на эту прямую. Существует и другой подход к поставленной задаче. На прямой произвольным образом выбираются две точки , и образовывается треугольник . Далее остается найти высоту полученного треугольника, проведенную из вершины .

Рассмотрим алгебраический подход к данной задаче. На прямой возьмем произвольную точку и рассмотрим квадрат расстояния между точками и

.

Для объяснения дальнейшего решения, напомним некоторые факты, связанные с прямыми в пространстве.

Каноническое уравнение прямой, проходящей через точку параллельно направляющему вектору

.

Параметрическое уравнение прямой, проходящей через точку параллельно направляющему вектору

При изменении параметра от до точка пробегает всю рассматриваемую прямую. Числа характеризуют направление прямой линии в пространстве, их называют направляющими коэффициентами прямой.

Для дальнейшего решения применим параметрическое уравнение прямой. В этом случае вместо трех неизвестных , и получим только одно неизвестное . Квадрат расстояния между точками и примет вид

.

Теперь остается найти минимальное значение функции и вычислить корень квадратный полученного минимального значения, т.е.

.

Для нахождения минимального значения функции достаточно вычислить значение этой функции в точке минимума.

Рассмотрим конкретный пример. В найти расстояние от точки до прямой, проходящей через точки и .

Решение. Составим параметрическое уравнение прямой , проходящей через точку , параллельно вектору

Таким образом, произвольная точка прямой имеет координаты

Квадрат расстояния между заданной точкой и произвольной точкой прямой

.

Находим производную

.

Решаем уравнение

.

Очевидно, что в точка является точкой минимума.

.

.

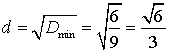Можно сделать вывод, что предложенный метод нахождения расстояния от точки до прямой в пространстве достаточно прост. Мы считаем, что данный метод следует довести до студентов и школьников.

Литература

1. Бронштейн И.Н., Семендяев К.А. «Справочник по математике», 1981.

2. Корн Г., Корн Т. «Справочник по математике для научных работников и инженеров», 1974, 720 с.