д.ф.-м.н. Павлов В.А., Лебедев С.В.

Санкт-Петербургский государственный университет, физический факультет, Россия

Аналитические оценки нелинейных эффектов над эпицентром землетрясения или мощного взрыва

Оценка величины энергии выделяемой в очаге землетрясения была произведена с использованием обширных эмпирических сейсмических данных о пространственно – временных характеристиках движения поверхности Земли в эпицентре. Для определения доли энергии, поступающей в атмосферу, и для выявления наиболее типичных закономерностей влияния сейсмических явлений на атмосферу введено понятие упрощенного «эталонного сейсмического явления». В основу его положена модель точечного источника, помещенного в атмосфере на высоту (где - пространственный масштаб неоднородности атмосферы) и проведено задание вида профиля положительной фазы движения (фазы сжатия) в источнике[1-2]. 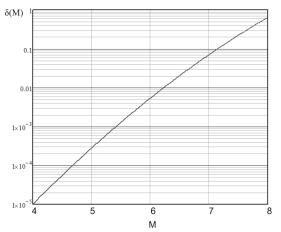Используя данные [3,4] о связи полного выделения энергии при точечном взрыве в воздухе и видом профиля положительной массовой скорости на уровне поверхности Земли удается получить оценочную формулу для доли энергии землетрясения , выделяемой в атмосферу, в зависимости от значений магнитуды M. Зависимость изображена на Рис.1.

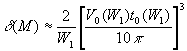, где W₁ (в килотоннах тротилового эквивалента)– энергия, выделяемая в очаге, V₀ (W₁) – амплитудное значение скорости поверхности земной коры в эпицентре, t₀ (W₁) – характерное значение периода положительной фазы движения. Коэффициент 2 связан с учетом вклада фазы разряжения, π – с использованным для аппроксимации конкретным видом зависимости профиля

Для описания начальной стадии нелинейной эволюции до той высоты, где влияние диссипации становится равноправным фактором, воспользуемся процедурой предложенной, независимо друг от друга, Ландау Л.Д. [5] и Уиземом Дж. [6] для приближенного описания нестационарных одномерных ударных волн малой интенсивности в средах без дисперсии и без диссипации. В основе метода лежит специальная модификация решения линейного приближения. При этом описание «геометрических» эффектов используются без изменений из линейного приближения для «простых» волн. Влияние нелинейности учитывается при замене ,где функция характеризует смещение атмосферы на уровне над эпицентром сейсмического источника, - неизвестная функция. Она вводится таким образом, чтобы для нелинейных волн малой интенсивности получить первое приближение по малому параметру , - линейная скорость звука, -скорость среды. Здесь - это локальное число Маха. Удобство такого описания заключается в том, что положение волнового фронта находится независимо от решения задачи в целом.

Рис.1	Рис.2

На Рис.2 изображена диаграмма зависимости , где z(М) представлена в метрах. В зоне 1 влияние нелинейности на эволюцию пренебрежимо мало. Таким образом, для землетрясений с магнитудой атмосферные возмущения могут описываться линейной теорией. Сплошная линия на Рис.2 характеризует уровень на котором сформировывается ударная волна. В зоне 2 ниже линии происходит непрерывная нелинейная трансформация акустического импульса. Здесь роль диссипации пренебрежимо мала. При эволюции импульса может формироваться «треугольный профиль». Пунктирная линия характеризует высоту , начиная с которой диссипация становится преобладающим фактором. В зоне 3 влияние диссипации и нелинейности равноправны. В зоне 4 диссипация преобладает над проявлением нелинейности.

На основе полученных представлений можно провести характеристику сейсмических явлений по величине нелинейных эффектов, возникающих в атмосфере.

I класс. - влияние нелинейности на процессы в атмосфере оказывается пренебрежимо малым по сравнению с влиянием других факторов.

II класс. - проявляются слабые нелинейные явления, в атмосфере происходит формирование слабой ударной волны.

III класс. - происходит формирование и эволюция сильных ударных волн в атмосфере

Литература

1. Павлов В.А. Акустический импульс над эпицентром землетрясения // Геомагнетизм и аэрономия. 1986, Т.26, №5, С.807-815.

2. Лебедев С.В., Павлов В.А. Компьютерное моделирование воздействия землетрясений и мощных взрывов на атмосферу // Вестник СПбГУ, 2009, сер.4.Физика, химия, Вып.1, С.52-61.

3. Броуд Г. Пространственные распределения давления, плотности и массовой в ударной волне при точечном взрыве в воздухе. Статья в сборнике: Г. Броуд Расчеты взрывов на ЭВМ. М., Мир 1976, С. 71.

4. Безрученко Л.И., Павлов В.А. Пространственно-временные характеристики возмущений атмосферы и ионосферы над эпицентром землетрясения // Вестник СПбГУ. 1997, Сер.4, Физика, химия. №25, С.138-141.

5. Ландау Л.Д. Об ударных волнах на далеких расстояниях от места их возникновения // Прикл. Матем. и мех. 1945,Т. 9, С. 286-300.

6. Уизем Дж. Линейные и нелинейные волны. М.: Мир,1977.