Технические науки / 2. Механика

к. т. н. Обухов А.Н., к.ф.м.н. Колесников С.А., Абакумов Д.С.

Донбасская государственная машиностроительная академия

О реализации периодических ударных колебаний одной сложной механической системы

 

 

                               Упругий шарик массой m падает с заданной высоты  на движущуюся преграду. Требуется подобрать параметры движущейся преграды, исходя из условия, что дальнейшее движение шарика при ударах о преграду будет периодическим с заданной амплитудой . Предполагается, что шарик движется под действием силы сопротивления пропорциональной квадрату скорости. Преграда перемещается вертикально. Удар о преграду упругий  с коэффициентом восстановления . Исследование поставленной задачи рассмотрим в три этапа.

 

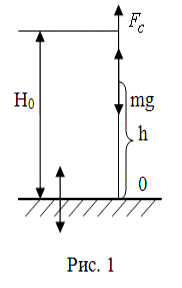
Первый этап. Движение шарика до удара об упругую преграду. Расчетная схема показана на Рис. 1.

 
 

 
 
        Дифференциальное уравнение движение шарика можно записать в виде 

                                                 ,                                               (1)                                                                      

            где =; h(t) - расстояние шарика до преграды;

 - скорость в момент времени t;

 - ускорение.

Найдем решение уравнения (1), удовлетворяющее начальным условиям:

                            h,        V                                          (2)                      

Разделяя переменные в уравнении (1) и интегрируя,     найдем:

 

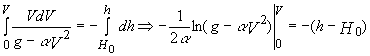             ,                          (3)

             Отсюда                                        

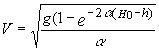                                                                                            (4)

Выражение (4) закон изменения скорости от высоты падения (H0-h). Полагая в (4) h=0 найдем V1-скорость шарика в момент удара о преграду

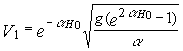                                                                            (5)

Используя равенство (4) запишем дифференциальное уравнение, и начальное условие для нахождения зависимости высоты от времени:

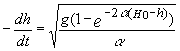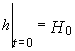                                       ,                    (6)

Разделяя переменные и интегрируя, получим

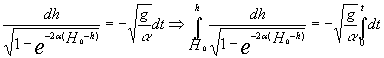                                    (7)

Вычисляя интегралы в левой и правой частях равенств, получим

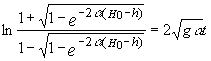                                                 .                     (8)

Разрешая равенство (8) относительно h, найдем закон изменения высоты шарика в виде

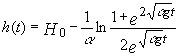                                                                              (9)

Полагая в равенстве (9) или (8) h=0,найдем формулу для вычисления t1 - время удара шарика о преграду

                                                              (10)

 

Проанализируем полученные результаты. Переходя в равенствах (4), (9) и (10) к пределу при → 0, получим известные школьные формулы

                                                                          h=-                t1=            

Здесь=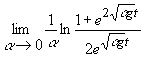

удерживая в  

         ( удерживая

 =  

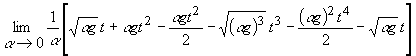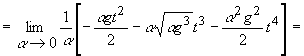
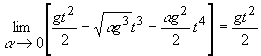
Второй этап. Рассмотрим движение шарика после удара о плиту. Пусть в результате удара о движущуюся преграду в момент времени t1, шарик мгновенно приобретает V2 - скорость, направленную вертикально вверх. Найдём закон изменения скорости от высоты подъёма, зависимость высоты подъёма как функцию времени, а также величину скорости V2,  при которой шарик поднимается на наибольшую высоту Н0 и время достижения этой высоты.

 

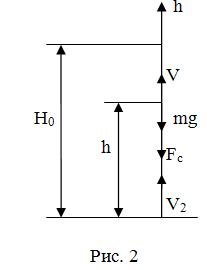
 Рассмотрим расчетную схему движения шарика после удара о плиту на Рис. 2.

          Математическая модель рассматриваемого процесса представляет собой дифференциальное уравнение

                                                                                                                           (12)                                            

С начальными условиями .                                        (13)        

Разделяя переменные и интегрируя, запишем

                                  

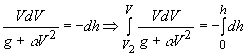
Вычисляя интегралы, получим

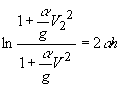                                                                                                                                      (14)  

Разрешим (14) относительно V (h)

Здесь:

                           ;

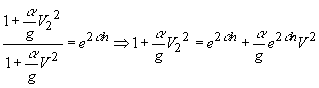отсюда               =;

окончательно получим,               V=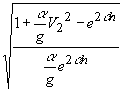-                            (15)

зависимость скорости шарика от высоты подъёма

Полагая в равенстве (15) скорость V=0 и h=H0, получаем формулу для вычисления V2 в виде

                                               V2=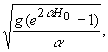                                    (16)

скорость, при которой шарик поднимается на наибольшую высоту H0                                                                                                                                                                                           

                                               V=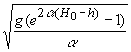                                  (16а)

Закон изменения скорости от высоты подъема (16a).

Найдём зависимость высоты подъёма как функцию времени. Для этого найдём решение дифференциального уравнения

                                                    ,                                 (17)

которое удовлетворяет начальным условиям:

                                                     

Разделяя переменные и интегрируя, найдём

                                     

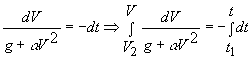
Вычисляя интегралы в правой и левой части равенства, найдём

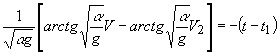                                                      (18)

отсюда

                                      и

                                    

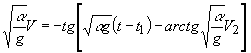
окончательно

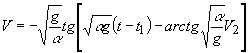                                                            (19)

Учитывая, что , получим дифференциальное уравнение

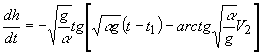                    ,                                     (20)

с начальным условием .

Разделяя переменные и интегрируя, найдём:

                     ,

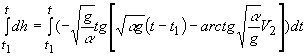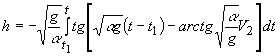                                                      (21)

Вычисляя интеграл, стоящий в правой части равенства, найдём:

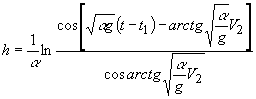                                                           (21а)

окончательно

                                            (22)

зависимость высоты подъёма шарика как функция времени t.

Из (21а) видно, что наибольшая высота подъёма H0 достигается в момент времени.

                                                                      (23)

Проанализируем полученные результаты, перехода в равенствах (16), (22) и (23), к пределу при получим известные школьные формулы.

;                             (24)  

Здесь:

;

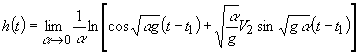  учитывая очевидные эквивалентности, найдем при

              

 = .

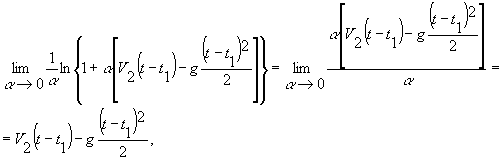
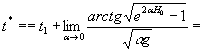
Третий этап. Выбор необходимых параметров движущейся преграды и периодического закона движения шарика.

Пусть преграда движется по гармоническому закону

                                     ,                                                     (25)

Здесь  - период колебания преграды или время между соседними ударами шарика о преграду; *- скорость преграды в момент t = t1

Найдём значение  при котором ударные колебания шарика будет периодическими с амплитудой Н0 и периодом

Согласно (25) скорость преграды

                                                                             (26)

В момент времени t = t1 скорость преграды равна * и направлена вверх.

Предположим, что в момент времени t = t1, шарик имеющий скорость  (см. (5), ударяется о неподвижную преграду, (удар считается упругим с коэффициентом восстановления (0 < r ≤ 1). После удара шарик меняет направление скорости на противоположное. Величина этой относительной скорости . Учитывая, что скорость шарика равна сумме относительной  и переносной скорости , т.е.

                                                                                   (27)

Учитывая выражение (5) и (16), найдём из равенства (27) значение необходимой  скорости преграды * в момент времени t1                    

                                                                         (28)

Найдём закон периодического движения шарика и преграды, принимая во внимание выражения (9), (22) и (25), уравнение движения шарика и преграды можно записать в виде:

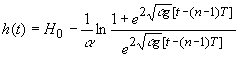,                                        (29)

(30)
 
                                 

                                                  

                                (31)

                    Где  и T=t* - находим по формулам (10) и (23)

                    n=1,2,3… - число ударов шарика о преграду

Замечание: пусть , переходя к пределу в равенствах (29), (30) и (31), получим известные школьные формулы.

(32)
 
                                                    

              

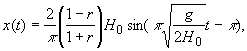
                                          (33)

                                 где  ,          ,          n=1,2,3…

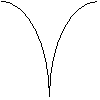
Графики колебательного процесса на одном периоде, при , представлены на Рис. 1  (движение преграды) и на Рис. 2 (движение шарика).

                

x(t)
 
                                                                          h(t)

 

 


         

t
 

t
 
 


T
 

T
 

0
 

0
 
                                                                                 

                      

Рис. 1
 

Рис. 2
 
 

 


Графики колебательного процесса на одном периоде, при (, g=10, r=0,9) представлены на Рис. 3 и Рис.4:

 

    t
 

2
 

h(t)

 
 

x(t)
 

t
 
           

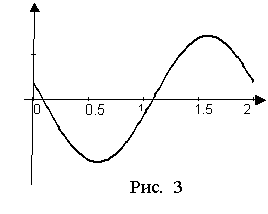
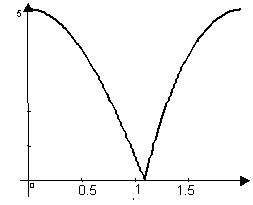
Рис.  4
 
 


 
 
Выводы. В работе показано,  существуют значения амплитуды и частоты движения преграды, когда в рассмотренной механической системе возможны периодические ударные колебания упругого шарика. Проведен графический анализ колебательного процесса на одном периоде в двух случаях. В случае, когда сопротивление среды отсутствует, время падения шарика стремится к значению равному половине периода движения. Если коэффициент сопротивления среды имеет конечное значение, тогда время падения шарика до удара о преграду увеличивается и смещается вправо относительно точки полупериода. В дальнейшем предполагается проанализировать зависимость времени падения от коэффициента сопротивления среды.

Литература:

1.        Обухов А.Н., Дмитренко И.С. Об ударных колебаниях упругого шарика, движущегося под действием силы сопротивления, пропорциональной квадрату скорости (амплитудная характеристика). MATERIALY 7 MIEDZYNARODOWEJ NAUKOWI-PRAKTYCZNEJ KONFERENJI “WSCHODNIE PARTNERSTWO-2011”, 07-15 WRZESNIA 2011 roku, Volume 6, Techniczne nauki, с. 18-21.

2.        Никитин Н.Н., Добронравов В.В. Курс теоретической механики. М.: Высшая школа, 1983, 575 с.

3.        Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М.: Наука, 1964, 272с.