Канд. техн. наук П. В. Терелянский

Волгоградский государственный технический университет, Россия

ЧИСЛЕННЫЙ МЕТОД ПРОГНОЗИРОВАНИЯ ДИНАМИКИ ПРИОРИТЕТОВ

В современных быстроменяющихся экономических условиях критерием оптимальной деятельности предприятий всех организационно-правовых форм давно перестало быть стремление к максимизации прибыли за счет минимизации производственных и организационных издержек. Разрабатывая концепцию развития бизнеса, экономисты все чаще стремятся учитывать не только классические индексы и индикаторы, но и такие трудно формализуемые понятия как экологичность, эргономичность, визуальная привлекательность, политическая и социальная конъюнктура и тому подобные. Как правило, оценка таких критериев связана с анализом неполных, непараметрических и слабоструктурированных экспертных знаний. Следовательно, требуется развивать математический аппарат и методики его применения, требуется разрабатывать информационные технологии и инструментальные средства для повышения оптимальности управленческих решений на всех уровнях экономики[1]. Универсальные программные системы поддержки принятия решений являются мощной инструментальной базой анализа подобных экономических процессов и систем. Принять оптимальное решение – значит выбрать такую альтернативу из числа возможных, в которой с учетом всех разнообразных факторов будет оптимизирована общая ценность. Оценка стратегии (или, вообще говоря, сценария, объекта, альтернативы, решения) по многим критериям означает, что эксперт преследует более чем одну цель, и эти цели могут иметь разную степень важности. При этом характерна несводимость критериев естественным образом к одному содержательно значимому показателю качества. Задача принятия решений в условиях неопределенности сводится к выбору оптимальной стратегии в операции, исход которой помимо стратегий оперирующей стороны и ряда фиксированных факторов зависит также от некоторых неопределенных факторов, неподвластных оперирующей стороне и неизвестных ей в момент принятия решения, а так же факторов, меняющихся со временем. Стратегии оперирующей стороны (альтернативы) x_i, i=1,n, в общем случае могут представляться скаляром, вектором, матрицей или еще более сложным образованием. Рассмотрим случай, когда стратегия оперирующей стороны представляется n-мерным вектором X=(x₁,x₂,…,x_n), а эффективность действий оперирующей стороны оценивается множеством локальных критериев качества K=(k₁,k₂,…k_m), интенсивность воздействия которых на общую систему W=(w₁,w₂,..w_m). Всякий локальный критерий k связан со стратегией (альтернативой) отображением f=F{X,A}, кроме того, всякий критерий связан со множеством других критериев отображением g=G{K,A}, где A – множество фиксированных факторов. Таким образом, многокритериальная задача принятия решений описывается следующим набором информации S=(X,K,W,F,G,P), где P – постановка задачи или цель исследования. Здесь уместно выделить из системы S подсистему предпочтений (критериев качества) S_p=(K,W,G), которая часто исследуется отдельно от множества альтернатив, например, когда в техническом задании определяется набор ограничивающих факторов (габариты, вес, мощность и т.д.), а инженеры на местах решают задачу максимизации соответствия нескольких вариантов устройств предоставленным ограничениям. Со временем могут изменяться как свойства исследуемых стратегий (альтернатив), так и свойства самой системы предпочтений S_p. В первом случае только отображение F есть функция времени, во втором только отображение G. Кроме того, возможен вариант, когда отображения G и F есть функции времени. Как найти оптимальное решение в этом случае? Принцип оптимальности решения представляет собой математическую модель принятого в задаче принципа компромисса. Перед анализом схемы компромисса обычно предполагают, что все локальные критерии нормализованы (т.е. имеют одинаковую размерность или являются безразмерными величинами). Альтернативы, которые имеют однотипные количественные характеристики, приводятся к одинаковой размерности путем линейного нормирования. Линейное нормирование заключается в том, что количественные величины заполняют собой вектор W'={w₁',w₂',..,w_n'},

где n – число альтернатив, а w'_i – количественная величина. Затем вектор W' нормируется, и в результате получается вектор приоритетов W={w₁,w₂,..,w_n},

где w_i=w'_i/S, а . Причем, если мы ищем лучшую альтернативу с наибольшей величиной данной характеристики, то вектор нормируется непосредственно с этими количественными оценками, а если наоборот (чем меньше данная величина, тем лучше), то каждый элемент вектора W' заменяется на обратную ему величину и только после этого происходит нормирование. Одним из способов нормализации неколичественных локальных критериев является метод парных сравнений. Пусть A₁, A₂, ...,A_n – множество из n элементов (альтернатив) и v₁,v₂,...,v_n – соответственно их веса или интенсивности. Эксперт выносит n(n-1)/2 суждений и формирует квадратную матрицу, содержащую парные сравнения, где n – порядок матрицы равный числу сравниваемых элементов. В этом случае матрица парных сравнений [A] имеет следующий вид:

.

Матрица парных сравнений обладает, как правило, свойством обратной симметрии, то есть a_ij = 1/a_ji, так как a_ij = v_i /v_j. Обратная симметрия выражается либо в виде правильной дроби, либо в виде отрицания прямой оценки a_ij=-a_ji. Числовая величина отношения v_i/v_j для неколичественных параметров обычно выражается с помощью некоторой вербальной шкалы, элементам которой поставлен в соответствие определенный числовой ряд. Возможно использовать выражения типа «Равное превосходство» или «Значительное превосходство». Каждой из таких вербальных оценок соответствует число от 1 до 9. Со временем могут изменяться не только субъективные показатели парных оценок элементов, но и их объективные веса. Например, со временем может вырасти цена объекта, измениться его масса, уменьшится длина и так далее. Если изменение данной метрической величины соответствует какой-либо закономерности, то для количественной оценки вполне можно подобрать функциональное представление этой закономерности и получить изменение вектора приоритетов во времени. Таким образом, в данный определенный момент времени в функциональные определение весов альтернатив подставляется значение момента времени и рассчитывается приведенный к единице вектор приоритетов. Аппроксимируя точки в полученном массиве векторов можно получить функциональное представление динамики предпочтений[2,3]. Данный подход позволяет использовать для принятия решений статистическую информацию.

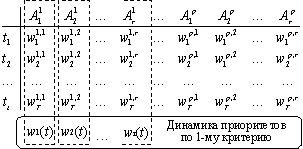
Рис. 1. Численный метод прогнозирования динамики приоритетов

На рисунке (рис. 1) верхний и нижний индексы Aⁱ_j обозначают, что j-ю альтернативу оценивали по i-му критерию, где r – количество альтернатив, p – количество критериев. Индексы элемента вектора приоритетов показывают, что w есть вес j-й альтернативы по i-му критерию в k-й момент времени, где k=1,...,T, а T – количество моментов времени. При исследовании поведения системы на больших промежутках времени мощность множества w(t) позволяет проводить регрессионный анализ. В результате можно получить функциональное представление динамики приоритетов альтернатив по какому-либо критерию. Изменение суждений можно оценить экспертно с использованием следующих функций. Постоянное увеличение одного вида деятельности по сравнению с другим – a₁×t+a₂. Быстрое увеличение (уменьшение) важности, за которым следует медленное увеличение (уменьшение) – a₁×ln(t+1)+a₂. Медленное увеличение (уменьшение) важности, за которым следует быстрое увеличение (уменьшение) – a ₁×exp(a₂×t)+ a₃. Увеличение (уменьшение) важности до максимума (минимума), затем уменьшение (увеличение) – a₁×t²+a₂×t+a₃. Колебания важности с увеличивающейся (уменьшающейся) амплитудой – a₁×t^a2×sin(t+a₃)+a₄. Параметры a_i этих функции можно установить так, чтобы область допустимых значений не выходила за границы установленных интервалов на рассматриваемом временном отрезке T. Эти функции отражают изменения в тренде: постоянном, линейном, логарифмическом и экспоненциальном, параболическом, а также колебательном. Анализ результирующих глобальных векторов приоритетов (после иерархической свертки) позволяет строить прогноз поведения исследуемой системы предпочтений.

Литература:

1. Терелянский, П.В. Информационные технологии прогнозирования технических решений на основе нечетких и иерархических моделей : монография / П.В. Терелянский, А.В. Андрейчиков. – Волгоград : ВолгГТУ, 2007. – 204 с.

2. Терелянский, П.В. Информационные технологии прогнозирования технических решений на основе иерархических моделей : монография / А.В. Андрейчиков, П.В. Терелянский, О.Н. Андрейчикова.– Волгоград : ВолгГТУ, 2004. –156 с.

3. Терелянский, П.В. Нечеткие модели и средства для принятия решений на начальных этапах проектирования : монография / А.В. Андрейчиков, П.В. Терелянский, А.М. Шахов. – Волгоград : ВолгГТУ, 2004. –140 с.