Quantification of the population education potential and its economic relations

Ladislav Kulčár

M. Bel University Banská Bystrica, Faculty of Economics

Institute of managerial systems, Branch Poprad, Slovakia

1. Introduction

In the economic theory a human capital is a specific form of a wider term capital that in general stands for accumulated or invested values and savings that can bring other values. In contrast to human capital the term of human potential is used mostly in the field of sociology as the ability of a man to create activities in a social community.

One part of human potential is a qualification potential that was reached by an individual in the process of formal institutional school education. A wider term is the term of educational potential that in contrast to a qualification potential includes also abilities of a man obtained in another forms and ways which differ from the process of improving qualification, that belong to the institutional system of education. Because the above-mentioned definition is related to every human being (individual member of a society), it can be called as an educational potential of an individual (EPI). In the economic theory the educational potential of a society (EPS) plays more important role that can be considered as a sum of the EPI´s of all the members of a society. Under the term a „society“ , in general, we can understand various kinds of societies or groups of people, e.g. people in a town, region, state, firm, institute or even people all over the world. The use of this term depends on our task.

The question arises how to measure EPS. One of the approaches how to measure it, is to take into consideration level of education, which can be expressed by the average length of education of the population in a given region, area, society or state [1]. The other approach, which has been used and discussed in [2] and [3], is to compute EPS according to the formula based on the relative frequency distribution of education within the population. The aim of this paper is mutually to compare these two approaches and find some economic relations between them.

2. Education potential of a society

Education potential of a society (EPS) has been introduced by Kulčár in [2] in the following form:

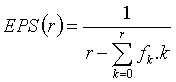, (1)

where k is an integer (k = 0, 1, …, r ) and it represents a serial number of the education level ordered in an ascending scale in the following way: no education, i.e. without any education (even illiteracy) = 0, basic education = 1, …., the highest education level, which equals r. The value allocated to the highest type of education is r = max{k}. The symbol f_k stands for the relative frequency of the k-th education level in the society. For computing the EPS we have to know frequency distribution f_k of a population based on the individual types of the highest institutionally achieved education. In dependence on a type of a society and time, the above-mentioned scheme can be changed from time to time and from region to region, e.g. after incorporate the another new forms of education into the educational system (e.g. lifelong education, etc.) or when some other supplementary forms of educational activities exist.

We can see from the Equation (1) that the value of EPS depends on the value of r. The value of r expresses the highest level of the education that can be reached in a considered society. Theoretically, the EPS ranges from the value of 1/r up to the infinity (∞). For Slovkia, theoretically, it ranges from 1/7 up to the infinity (see below). The fact, that the value of EPS can increase up to the infinity, is the consequence of the similarity of the Eq. (1) for EPS with the rational function of the following form

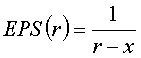(2)

With the vertical asymptote (discontinuity) at x = r (r = 7 for Slovakia, see below) (Figure 1). This extreme case could theoretically occur, when the structure of the frequency distribution in the society would be, that all individuals of the society reach the highest possible education level in the formal institutional educational system. The fact, that the EPS values strongly depend on the shift of the mode of the frequency distribution to the larger k values, can indicate the synergic non-linear effects. Deeper theoretical discussion of this problem is published in the paper [2].

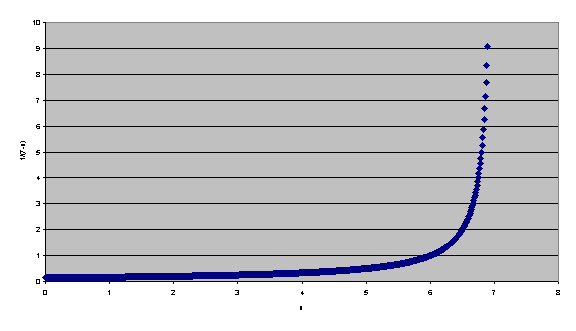
Figure 1: EPS(r) expressed as a function of 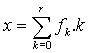for Slovakia (r =7).

The fact, that EPS(r) depends on the value of r, can be considered as a disadvantage of this method for evaluation of the education potential. Different countries have their own educational systems and the consequence of this is that we can effectively compare using the EPS only the systems with the same value of r as the highest reached institutional education level. But, on the other hand, we can effectively compare the changes of the EPS, which have occurred in time in a given society or a region. For example, for Poprad district situated in the northern part of Slovakia we obtained, using the data published in [4], the EPS value equals 0,266 for 1980 and the value of 0,293 for 1991, consequently. These two values clearly indicates that the education potential of the Poprad district got higher from 1980 to 1991.

3. Application of the EPS for Slovakia

We calculated the EPS values for 79 regions (districts) of Slovakia. The data on relative frequency distribution of the highest reached education level of the population gathered by the Statistical Office of the Slovak Republic in the population and housing census in 2001 [5] were used. There are at disposal the data on the frequency of the population with the highest reached education level per 1000 inhabitants, whereas the education level is specified in the following categories:

A. Elementary (primary) education level (including unfinished)

B. Education level (apprentice schools) without General Certificate of Education (GCE) exam

C. General secondary and comprehensive school with GCE exam

D. Post-secondary specialized vocational qualificatory school with GCE exam – the second GCE exam

E. Bachelor (college) level – the 1^st step of the high school education

F. University education level (degrees magister - Mgr., engineer - Ing., doctor – Dr.) – the 2^nd step of the high school education

G. Higher university education level (degree PhD) – the 3^rd step of the high school education

H. Bachelor, university and higher university education level together (E + F + G)

I. People without any education level

J. People without information on their education level

K. Children younger than 16 years.

For our purpose we used the above-mentioned data on education level of the population in a little modified form. The values of k than used in the Eq. (1) were created in the following way:

k = 0 – the lowest category of the education level: people without any education

level (category I),

k = 1 – people with elementary (primary) education level (including unfinished)

(category A),

k = 2 – people with education level without General Certificate of Education

(GCE) exam together (apprentice and specialized schools) (category B),

k = 3 – people with general secondary and comprehensive school with GCE

exam together (category C),

k = 4 – people with post-secondary specialized vocational qualificatory school

with GCE exam (category D),

k = 5 – people with bachelor (college) education level – the 1^st step of the high

school education (category E),

k = 6 – people with university education level – the 2^nd step of the high school

education (category F),

k = 7 – people with higher university education level – the 3^rd step of the high

school education (category G).

In our calculation we used the data concerned only economically active people and people older than 16 years. The values of EPS are in the first column of Table 1.

4. Educational potential expressed by ALE

A different approach how to measure the EPS is to use an average length of education (ALE). The average length of education is defined as the number of years, on average, an individual (student) remains at the institutions providing formal institutional education (i.e. schools and universities of various types), including years spent on repetition. The average length of schooling shows an educational system´s overall level of development. This value is the sum of all lengths of schooling expressed in years up to the moment when an individual reaches his/her highest level of education.

Fischer and Mazouch [1] used as a measure of the level of education the average length of education of the population in a given region. They used data on the highest attained level of education from the housing and population census done by Czech Statistical Office in Czech Republic in 1991 and 2001. They computed an average length of education of the population from these raw data using the length necessary for an absolutory of a given education level.

The same methodology for computing the average length of education was used by us for 79 regions in Slovakia. Our results are based on the data gathered and published by the Statistical Office of Slovak Republic in 2001 [5]. We want to compare the results obtained by the both methods for 79 regions of Slovakia, so we used the same categories for the highest attained education level as we have used for computing the EPS values. In our case we used the following lengths of education characterized by the length necessary for an absolutory of a given level:

Category I (k = 0) : 0 years

Category A (k = 1) : 8,6 years

Category B (k = 2) : 11,6 years

Category C (k = 3) : 12,4 years

Category D (k = 4) : 14,4 years

Category E (k = 5) : 15,4 years

Category F (k = 6) : 17,5 years

Category G (k = 7) : 21,5 years

Symbol l_k (expressed in years) we will use for the lengths of education given above. These values are in their nature the weighted average values of the lengths of education, because in each category of education level are considered people of different ages and they are represented in each category by different relative frequencies. For example, the length of education for the level k = 1 (obligatory basic education) have been changed in time in Slovkia, resp. Czechoslovakia as follows: in period 1928 – 1948 l₁ = 8 years; in 1948 – 1953 l₁ = 9 years; in 1953 – 1960 l₁ = 8 years; in 1960 – 1978 l₁ = 9 years; in 1978 – 84 l₁ = 8 years; in 1984 – 1990 l₁ = 10 years; in 1990 – 1997 l₁ = 9 years; in 1997and up today l₁ = 10 years [6]. And moreover, we have to take into consideration the fact, that in the population of people with basic education as the highest reached education level are included also people born in the first half of the last century, whose length of basic education was less than 8 or 9 years. The resulted values of the length of education for the given levels of education are just rough esitmates based on the mentioned relations and considerations.

In the next we computed the average length of education (ALE) for every region of Slovakia as a weigthed arithmetic mean of individual lengths of education l_k. The weights f_k were taken the relative frequencies of occurrences of the given education level in the population in a given region. So, for ALE we have:

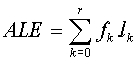, (3)

where k has the same meaning as in the Eq. (1) and r = 7 for Slovakia. The ALE values for 79 districts of Slovakia are in the second column of Table 1.

Our purpose is now to find the mutual relation between the above-mentioned two measures of education level, i.e. the EPS defined by Eq. (1) and the ALE defined by Eq. (3). For this reason we used the least square method, where the ALE stands for an explanatory (independent) variable and the EPS stands for an explained (dependent) variable. We found that the best fit function for this relation for Slovakia is the polynomial function of the degree 2, and so we could write:

(4)

with the coefficient of determination 99,06 % (Figure 2).

From the close relation between EPS and ALE values we can conclude, that it is, in principle, the same, which one of these two measures will be used for the

Table 1: Educational potential (EPS), average length of education (ALE) and the rate of unemployment for 79 districts of Slovakia in 2001.

District	EPS	ALE (in years)	Rate of unemployment (in %)
Bratislava I	0,36258	14,6153	7,71
Bratislava II	0,28514	13,3473	9,03
Bratislava III	0,29455	13,5675	7,97
Bratislava IV	0,30798	13,8487	7,18
Bratislava V	0,27345	13,1407	10,59
Malacky	0,22198	11,7563	15,36
Pezinok	0,23998	12,3057	9,95
Senec	0,23469	12,1757	10,51
Dunajská Streda	0,21863	11,6811	20,52
Galanta	0,21959	11,7176	20,14
Hlohovec	0,22831	12,0591	18,17
Piešťany	0,24325	12,4641	13,03
Senica	0,22302	11,8605	17,57
Skalica	0,22202	11,8206	16,98
Trnava	0,24050	12,4034	15,30
Bánovce n/B	0,22883	12,1163	20,17
Ilava	0,23883	12,3462	12,53
Myjava	0,23026	12,0825	17,96
Nové Mesto n/V	0,23310	12,1734	14,47
Partizánske	0,22665	11,9456	21,35
Považská Bystrica	0,23855	12,3336	17,54
Prievidza	0,23004	12,0773	16,59
Púchov	0,23175	12,1327	13,75
Trenčín	0,24504	12,5249	11,17
Komárno	0,22139	11,7663	27,05
Levice	0,22836	11,9914	27,11
Nitra	0,24570	12,5445	18,02
Nové Zámky	0,22609	11,9281	25,44
Šaľa	0,22386	11,8695	22,77
Topoľčany	0,22883	12,0840	20,65
Zlaté Moravce	0,22831	12,0157	25,98
Bytča	0,22247	11,9188	17,98
Čadca	0,22188	11,8968	19,65
Dolný Kubín	0,24079	12,4115	21,39
Kysucké Nové Mesto	0,22831	12,0514	21,65
Liptovský Mikuláš	0,24290	12,4747	14,80
Martin	0,24624	12,5491	18,32
Námestovo	0,21668	11,6710	18,85
Ružomberok	0,23170	12,1587	19,07
Turčianske Teplice	0,22487	11,9711	18,27
Tvrdošín	0,23143	12,1186	20,45
Žilina	0,24832	12,6452	16,78
Banská Bystrica	0,26316	12,8880	12,99
Banská Štiavnica	0,23299	12,1177	20,32
Brezno	0,22660	11,9074	24,19
Detva	0,22614	11,9305	23,72
Krupina	0,22257	11,8591	23,93
Lučenec	0,22589	11,8314	29,14
Poltár	0,21906	11,6891	25,71
Revúca	0,21566	11,4402	33,88
Rimavská Sobota	0,21404	11,4925	36,43
Veľký Krtíš	0,22070	11,7156	33,20
Zvolen	0,25458	12,7075	16,43
Žarnovica	0,22894	11,9785	24,62
Žiar n/Hronom	0,23480	12,1433	20,12
Bardejov	0,22862	12,0457	25,49
Humenné	0,24044	12,4056	25,43
Kežmarok	0,21236	11,3278	31,71
Levoča	0,22095	11,6751	26,42
Medzilaborce	0,23068	12,0673	28,68
Poprad	0,23759	12,2294	20,62
Prešov	0,24588	12,5215	23,60
Sabinov	0,21867	11,6849	31,33
Snina	0,23041	12,0586	25,52
Stará Ľubovňa	0,21519	11,8347	20,88
Stropkov	0,22952	12,0382	26,90
Svidník	0,23079	12,0940	25,30
Vranov n/Topľou	0,22396	11,8689	28,98
Gelnica	0,21487	11,4566	25,65
Košice I	0,28531	13,3684	17,71
Košice II	0,25740	12,7595	19,19
Košice III	0,25195	12,6406	22,14
Košice IV	0,25720	12,7451	18,84
Košice okolie	0,21487	11,4544	28,17
Michalovce	0,23036	12,0131	32,37
Rožňava	0,21978	11,6154	29,18
Sobrance	0,21978	11,5932	32,43
Spišská Nová Ves	0,22341	11,6717	26,32
Trebišov	0,22031	11,6146	31,36

quantification of the education potential of a society. Of course, the statistical relation expressed by formula (4) is valid for Slovakia.

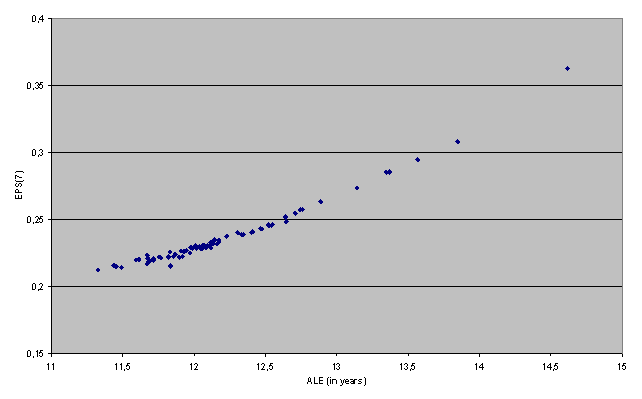
Figure 2: Relation between EPS(7) and ALE (in years) for 79 districts of Slovakia.

5. Educational potential and its economic relations and consequences

In this part we will compare the education potential expressed by ALE values and the measure of unemployment in Slovakia in 2001 based on the data published in [5]. The ALE parameter as a measure of the education potential was preferred instead of the EPS parameter because of the much more illustrative value than the EPS value. The rate of unemployment is calculated in relation to the economically active people. The rate of unemployment for 2001 in 79 district of Slovakia is in the third column of Table 1.

The next step of our research was to find a model which would describe the relation between the education potential expressed by ALE and the rate of the unemployment. Our model is based on their statistical relations which can be seen in Figure 3. This relation can be expressed by the following formula:

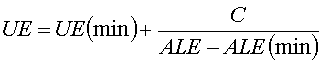, (5)

where UE stands for the rate of unemployment expressed in percentage, UE(min) is a minimum value (limit) of the unemployment, C is a constant and ALE(min) is a minimum value of the average length of education. We put 11 years for the ALE(min) value. The choose of this value was based on Figure 3. The UE(min) represents a theoretical minimum value of the unemployment rate in trade economy.

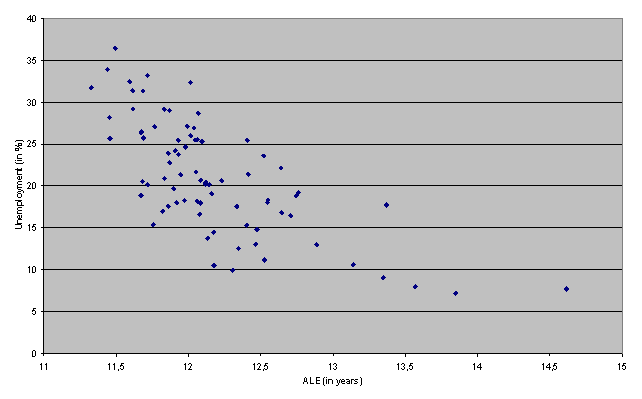
Figure 3: Relation between the rate of unemployment (in %) and ALE (in years) for 79 districts of Slovakia.

We put 5 % for this value, which is an estimate based on the real economic situation in stable economics. Using formula (5) and the real data from Table 1 for Slovakia we found the value of the constant C equals 16,1454. The values of C and ALE(min) can be different for different countries and their values depend on time, when the data were gathered. For example, the rates of unemployment displayed in Table 1 were calculated for 2001 and they are much higher in comparison with the unemployment rates in the same districts nowadays. Unemployment is more sensitive in time than the educationa potentials expressed by EPS or ALE values.

6. Conclusions

The aim of our paper was to compare two ways of expression and description of the education potential of a society. As a society was considered the Slovak Republic as a whole in our case. We found, that the level of education of the population can be represented by mutully close dependent two parameters: one as the EPS value and the second one as the ALE value. The statistical relation between them for Slovakia is given by Equation (4). Each of them has its advantages, on one side, and its disadvantages, on the other side. Because of the strong statistical relations between them it is up tu us which one of them will be used in practice. In practice, it will depend on the fact, which kind of data will be at our disposal.

In the next we found, that there is a statistical significant relation between education potential (expressed by one of these two indicators, i.e. EPS or ALE) and the rate of unemployment in a given society. The mutual relation between them can be modeled by the mathematical formula given by (5). In general, the model expressed by (5) can be applicated for various different countries, but the values of ALE(min), UE(min) (probably) and constant C can be different for each country. It may be interesting to compare the values of these parameters for different countries of the Middle and East-European Region, because these countries had been developing very similarly for a long time. They had/have similar educational institutional and economic systems, history, traditions and even mentality of people.

References:

[1] Fischer, J., Mazouch, P.: Level of Education and Gross Value Added: Analysis from the Regional Point of View. In: Applications of Mathematics and Statistics in Economy (AMSE), Proceedings of the 10th International Scientific Conference, Poprad, Slovakia, pp. 42-46, 2007, ISBN 978-80-969535-7-8.

[2] Kulčár, L.: Possibilities of population education potential quantification. In: Acta oeconomica No. 16 (Applications of Mathematics and Statistics in Economy), Faculty of Economics, M. Bel Universtiy Banská Bystrica, pp. 102-107, 2003, ISBN 80-8055-874-4.

[3] Kulčár, L.: Vzdelanostný potenciál populácie Slovenska a možné súvislosti. In: Proc. Of the 4^th International Conference Aplimat 2005, Faculty of Mechanical Engineering, Slovak University of Technology, Bratislava, Part II, pp. 493-500, 2005, ISBN 80-969264-2-X (in Slovak).

[4] Sčítanie ľudu, domov a bytov k 31. marcu 1991 v okrese Poprad, Okresné oddelenie Slovenského štatistického úradu v Poprade, Poprad, december 1992, pp. 150 (in Slovak).

[5] Sčítanie obyvateľov, domov a bytov 2001 (Bývajúce obyvateľstvo 15-ročné a staršie podľa vekových skupín a najvyššieho skončeného stupňa školského vzdelania na 1000 obyvateľov za SR, kraje a okresy, I. a II. diel), Štatistický úrad SR, Bratislava, Kód 0913103, s. 5 – 415 (I. diel), 5 – 355 (II. diel), 2003 (in Slovak).

[6] Obdržálek, Z., Horváthová, K. a kol.: Organizácia a manažment školstva. Terminologický a výkladový slovník. Slovenské pedagogické nakladateľstvo, Bratislava, pp. 419, 2004. ISBN 80-10-00022-1 (in Slovak).