Ершова Н.М., Шибко О.Н.
Приднепровская государственная академия
строительства
и архитектуры
АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ УСТРОЙСТВ
УПРАВЛЕНИЯ И ПЛАНИРОВАНИЯ ПРОЦЕССА ВЫПУСКА
ВАЛОВОГО ПРОДУКТА
Методы и средства представления объекта управления в технической кибернетике
образуют комплекс задач при аналитическом конструировании регулятора. Регулятор
– это устройство, оценивающее в каждый момент текущее состояние объекта и на
основе этой оценки вырабатывающее входные воздействия, которые выводят объект в
заданную точку пространства состояний. При этом реализуется принцип обратной
связи – текущее управляющее воздействие является функцией текущего состояния
объекта.
Задача
синтеза систем при случайных воздействиях и помехах называется задачей аналитического
конструирования устройств активного управления. Метод стохастического
динамического программирования содержит в своем алгоритме алгоритмы двух других
методов: динамического программирования для непрерывных детерминированных динамических
систем и оптимальных фильтров Калмана-Бьюси [1]. Следовательно, для разработки устройств управления, которые могли бы
полностью реализовать алгоритм стохастического динамического программирования,
решать задачу активного управления динамическими процессами следует поэтапно: вначале
спроектировать пассивную систему; затем, если необходимо, создать механизм
активного управления, реализующий закон управления или матрицу параметров
оптимального фильтра.
Аналитическое
конструирование устройств управления на основе метода стохастического
динамического программирования динамическими процессами экономических систем
представлено работе [2].
В этом методе математическая модель объекта
управления имеет вид:
 (1)
(1)
где ![]() – неизвестный вектор
состояния системы;
– неизвестный вектор
состояния системы; ![]() – вектор управления;
– вектор управления; ![]() – вектор входных
возмущений;
– вектор входных
возмущений; ![]() – вектор наблюдения;
– вектор наблюдения; ![]() – вектор ошибок измерений;
– вектор ошибок измерений;
![]() – вспомогательные
матрицы соответствующих размеров.
– вспомогательные
матрицы соответствующих размеров.
Входное возмущение и ошибки измерений выходных координат системы считаются
гауссовскими случайными процессами типа белого шума с нулевым математическим ожиданием.
Следовательно, их корреляционные функции принимаются в виде ![]() где d(t) –
дельта-функция Дирака;
где d(t) –
дельта-функция Дирака; ![]() – матрица,
элементами которой являются дисперсии входного возмущения;
– матрица,
элементами которой являются дисперсии входного возмущения; ![]() – матрица,
элементами которой являются дисперсии ошибок измерения компонент вектора
состояния. Начальное состояние системы представляет собой гауссовскую векторную
случайную величину, не зависящую от входного возмущения и ошибок измерительных
приборов, с математическим ожиданием
– матрица,
элементами которой являются дисперсии ошибок измерения компонент вектора
состояния. Начальное состояние системы представляет собой гауссовскую векторную
случайную величину, не зависящую от входного возмущения и ошибок измерительных
приборов, с математическим ожиданием ![]() и известной
корреляционной матрицей
и известной
корреляционной матрицей ![]() элементами
которой являются требуемые дисперсии выходных координат системы.
элементами
которой являются требуемые дисперсии выходных координат системы.
В качестве
критерия оптимальности принимается функционал
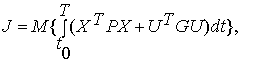 (2)
(2)
где ![]() – матрица весовых
коэффициентов, учитывающих весомость компонент вектора состояния;
– матрица весовых
коэффициентов, учитывающих весомость компонент вектора состояния; ![]() – матрица весовых
коэффициентов вектора управления; символ
– матрица весовых
коэффициентов вектора управления; символ ![]() означает операцию
математического ожидания; символ
означает операцию
математического ожидания; символ ![]() в выражении интеграла
– транспонирование матриц. Физический смысл функционала – удержать средние
значения компонент вектора состояния около положения устойчивого равновесия без
слишком большой затраты (энергии, денежных средств и др.) на управление.
в выражении интеграла
– транспонирование матриц. Физический смысл функционала – удержать средние
значения компонент вектора состояния около положения устойчивого равновесия без
слишком большой затраты (энергии, денежных средств и др.) на управление.
Ставится задача: определить закон управления по оценке вектора состояния
системы, полученной на основе измерения ее выходных координат на интервале
времени ![]() , доставляющий минимум функционалу.
, доставляющий минимум функционалу.
В соответствии с теоремой разделения оптимальное управление ![]() в системе,
представленной уравнениями (1), доставляющее минимум функционалу, имеет
следующий вид:
в системе,
представленной уравнениями (1), доставляющее минимум функционалу, имеет
следующий вид:
![]() (3)
(3)
где ![]() – обратная матрица;
– обратная матрица; ![]() - транспонированная матрица;
- транспонированная матрица; ![]() - оценка вектора состояния системы;
- оценка вектора состояния системы; ![]() – матрица–результат
решения матричного дифференциального уравнения Риккати:
– матрица–результат
решения матричного дифференциального уравнения Риккати:
![]() (4)
(4)
Оценка вектора состояния системы определяется из решения дифференциального
уравнения
![]() (5)
(5)
при ![]() В уравнении (5)
В уравнении (5) ![]() – корреляционная матрица
ошибки оценки, получаемая из решения дисперсионного уравнения типа Риккати:
– корреляционная матрица
ошибки оценки, получаемая из решения дисперсионного уравнения типа Риккати:
![]() (6)
(6)
Матрица параметров оптимального фильтра формируется из уравнения (5)
![]() (7)
(7)
Таким образом, стохастическое динамическое программирование позволяет
создать пассивную систему и ввести в нее активное управление по оценке вектора
состояния исследуемой системы.
Определим матрицу параметров оптимального фильтра для управляемого процесса
выпуска валового продукта фирмы
![]()
или ![]() (8)
(8)
где ![]() - объем внешних инвестиций
фирмы.
- объем внешних инвестиций
фирмы.
Представим уравнение (8) в форме Коши, принимая ![]()
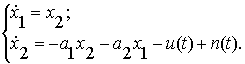 (9)
(9)
Опишем состояние системы в соответствии с методом
стохастического динамического программирования
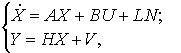 (10)
(10)
где

В качестве критерия оптимальности примем функционал качества:
![]() (11)
(11)
или в
матричной форме ![]() ,
,
где ![]() - весовые
коэффициенты функционала. Физический смысл функционала – средние затраты
денежных средств на поддержание стабильного функционирования фирмы.
- весовые
коэффициенты функционала. Физический смысл функционала – средние затраты
денежных средств на поддержание стабильного функционирования фирмы.
Матрицы
![]() функционала имеют
вид:
функционала имеют
вид:
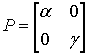 ;
; ![]() .
.
Закон
оптимального управления процессом выпуска валового продукта
![]() (12)
(12)
Матрица ![]() определяется из
системы дифференциальных уравнений типа Риккати
определяется из
системы дифференциальных уравнений типа Риккати
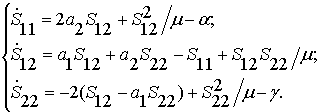
![]() (13)
(13)
Для определения
оценки вектора состояния процесса необходимо иметь корреляционную матрицу ![]() . В дисперсионное уравнение, из решения которого она получается,
входят матрицы
. В дисперсионное уравнение, из решения которого она получается,
входят матрицы ![]()
![]() ;
; 
где ![]() – дисперсия ускорения
ввода внешних инвестиций;
– дисперсия ускорения
ввода внешних инвестиций; ![]() – дисперсии ошибок измерений компонент
вектора состояния.
– дисперсии ошибок измерений компонент
вектора состояния.
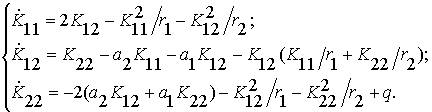 (14)
(14)
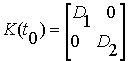 , где
, где ![]() - требуемые дисперсии
процесса выпуска валового продукта и производственной мощности фирмы.
- требуемые дисперсии
процесса выпуска валового продукта и производственной мощности фирмы.
Следовательно,
матрица параметров оптимального фильтра имеет вид:
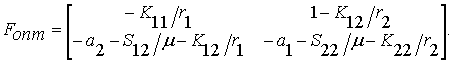 (15)
(15)
Рассматриваемый
пример характерен для модернизации действующих фирм. В расчетах, связанных с
проектированием новых фирм, необходимо принять матрицу ![]() из метода
динамического программирования для непрерывных детерминированных систем, т. е.
из метода
динамического программирования для непрерывных детерминированных систем, т. е. 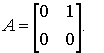
В экономических системах возникает проблема представления субъекта
управления. Субъект управления – это система, которая ставит и решает задачи.
В соответствии с принципом Беллмана процесс определения решений, протяженных
во времени, разворачивается из будущего в обратной временной
последовательности. Следовательно, если для объекта воспользоваться свойством
обратимости системы влево [3], то получим субъект управления.
Планирующее устройство (планировщик) и регулятор основаны на общих
принципах и роли их аналогичны. Подключенный к субъекту планировщик
осуществляет планирование, т.е. выявляет и формулирует цепочку промежуточных
целей субъекта. В процессе управления субъект и объект взаимодействуют, но не
напрямую, а путем взаимодействия планировщика и регулятора в форме реализации
плана или программы.
Для построения математической модели субъекта принята модель объекта.
без учета внешнего возмущения, т.е. на вход объекта поступает вектор управления
![]() - множество
управленческих воздействий, выходом является вектор
- множество
управленческих воздействий, выходом является вектор ![]() - вектор наблюдения,
т.е. математическая модель объекта имеет вид:
- вектор наблюдения,
т.е. математическая модель объекта имеет вид:
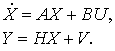 (16)
(16)
Объект управления представляется в виде черного ящика, вход и выход
которого можно непосредственно наблюдать и по ним оценивать текущее состояние ![]() для выработки
текущего входного воздействия
для выработки
текущего входного воздействия ![]() . Этим занимается устройство управления, которое по структуре
объекта (
. Этим занимается устройство управления, которое по структуре
объекта (![]() ) настраивается на него в процессе регулирования.
) настраивается на него в процессе регулирования.
Для системы (16)
использовано свойство обратимости влево. Для этого составлена сопряженная
система, в которой через ![]() - обозначен вектор
целевого состояния системы. Сопряженная система получается из исходной путем следующих
преобразований: обращение времени; перестановка матриц, связанных с входной и
выходной переменными; транспонирование матриц
- обозначен вектор
целевого состояния системы. Сопряженная система получается из исходной путем следующих
преобразований: обращение времени; перестановка матриц, связанных с входной и
выходной переменными; транспонирование матриц ![]() .
.
 (17)
(17)
Свойство
обратимости системы влево позволяет по ее выходу определить вход, т.е.
построить модель субъекта управления (18).
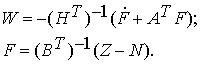 (18)
(18)
Назначение планировщика в этом случае состоит в оценке вектора целевого
состояния системы. Математическая модель планировщика строится по математической
модели устройства управления.
Для процесса выпуска валового продукта матрица параметров оптимального
планировщика имеет вид:
 (19)
(19)
Сравнивая матрицы (15) и (19)
отмечаем, что матрица ![]() по форме является
транспонированной по отношению к матрице
по форме является
транспонированной по отношению к матрице ![]() системы (10) и
системы (10) и ![]() , но матрица
, но матрица ![]() отличается от матрицы
отличается от матрицы
![]() знаками
присоединенных составляющих к элементам матрицы
знаками
присоединенных составляющих к элементам матрицы ![]() .
.
Литература:
1. Ершова Н.М. Оптимальное проектирование системы
подвешивания железнодорожных экипажей: дис. на соискание науч. степени докт.
техн. наук: спец. 05.22.07 «Подвижной состав железных дорог и тяга поездов» /
Ершова Нина Михайловна; Белорусский ин-т инж. ж.д. трансп. – Гомель, 1989. –
374 с.
2. Ершова Н.М. Моделирование динамических процессов экономических
систем: Конспект лекций / Н.М. Ершова. – Днепропетровск: ПГАСА, 2007. – 112 с.
1. Фильтрация
и стохастическое управление в динамических системах / Под ред. К.Т. Леондеса.
Пер. с англ. – М.: Мир, 1980. – 407 с.