Ершова Н.М., Герасименко С.В.

Приднепровская государственная академия

строительства и архитектуры

ПРОЦЕСС ВЗАИМОДЕЙСТВИЯ ФИРМ

В ПРОИЗВОДСТВЕННОЙ СИСТЕМЕ

Математическая модель производственной системы, объединяющей взаимодействующие простые производственные объекты, имеет вид [1]:

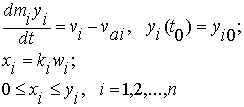(1)

где - соответственно поток выпуска продукции и производственная мощность - го объекта; - потоки поступления соответственно основных и оборотных производственных фондов на - й объект; - поток выбытия (амортизации) ОПФ - го объекта; - соответственно мгновенная фондоемкость ОПФ и мгновенный коэффициент эффективности ОбПФ - го объекта.

Влияние людей на производство осуществляется через затраченный труд, который входит составляющей в поток оборотных фондов.

Поток выбытия ОПФ достаточно полно моделируется линейной функцией

, (2)

где - коэффициенты выбытия ОПФ. Если поток выпуска продукции равен нулю, то оборудование не используется, но оно стареет и морально изнашивается, поэтому , т.е. износ пропорционален производственной мощности. Если оборудование эксплуатируется, то износ происходит быстрее и определяется уравнением (2). На самом деле процесс износа ОПФ значительно сложнее. На практике обычно принимают

, (3)

где при , т.е. поток продукции - го объекта равен его производственной мощности. При планировании выпуска той или иной продукции обычно нет смысла оставлять часть мощности недоиспользованной, поэтому следует принять , т.е. использовать полностью производственные мощности всех объектов.

Объекты модели (1) поставляют друг другу продукцию, т.е. взаимосвязаны. Предположим, что производственная система представлена двумя фирмами (рис. 1) [2], каждая из которых выпускает валовую продукцию и затрачивает на воспроизводство труд, средства труда и предметы труда. Здесь индекс определяет фирму. Валовая продукция каждой отрасли распределяется в блоках соответственно на конечную продукцию и производственное потребление :

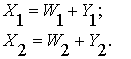
Рис. 1. Схема взаимодействия двух фирм

Производственные затраты каждой фирмы расходуются на воспроизводство валовой продукции обеих фирм и это распределение осуществляется в блоках : 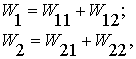где - межфирменные потоки из - ой фирмы в - ую. Если предположить, что межфирменные потоки пропорциональны объему валовой продукции, т.е. где - норма затрат продукции - ой фирмы на воспроизводство единицы продукции - ой фирмы, то распределение валовой продукции фирм можно представить в виде:

(4)

Блоки участвуют в межфирменном обмене производственных затрат и образуют систему межфирменных связей. Выделение этой системы из рассматриваемой модели приводит к модели межфирменного баланса, имеющей самостоятельное значение. Модель межфирменного баланса для двух фирм представлена на рис. 2.

В блоках происходит деление конечной продукции на валовые инвестиции и непроизводственное потребление:

(5)

Это приводит к вводу в балансовое уравнение составляющих связь которых с валовой продукцией выражается дифференциальными уравнениями.

В простейшей двухфирменной модели будем считать, что все валовые инвестиции идут на развитие производственной системы (не учитываем амортизационные отчисления) и их потоки пропорциональны приросту валовой продукции, т.е.

(6)

где - коэффициенты пропорциональности.

Расход валовых инвестиций каждой фирмы на увеличение основных фондов осуществляется соответственно в блоках :

(7)

Рис. 2. Модель межфирменного баланса

Подставляя в (4) выражения (5)-(7), получим математическую модель развития производственной системы [3], состоящей из двух фирм,

(8)

Для решения системы линейных неоднородных дифференциальных уравнений (8) необходимо иметь начальные условия, т.е. для базисного года значения и известные функции потребления Система (8) представляет собой открытую двухфирменную модель производственной системы.

Математическая модель производства и распределения продукта одной фирмы позволяет увязать основные экономические показатели: валовой продукт, конечный продукт, капитальные вложения (инвестиции), трудовые ресурсы, потребление и др. Для эффективного управления производственной системой, имеющей сложную структуру, необходимо установить плановые пропорции на фирменном уровне. Это движение общественного продукта на всех стадиях воспроизводства учитывает метод межфирменного баланса.

Межфирменный баланс служит базой определения взаимно сбалансированной системы основных показателей и отражает кругооборот общественного продукта в целом по производственной системе и на межфирменном уровне.

Идея межфирменного баланса состоит в следующем. Каждый производимый в производственной системе продукт должен быть рассмотрен с точки зрения его распределения и использования. С другой стороны, каждый продукт может быть представлен по элементам стоимости как сумма затрат различных продуктов, расходуемых на его изготовление (сырья, полуфабрикатов, топлива, электроэнергии и др.), амортизацию основных фондов, заработную плату создающих продукт работников и чистого дохода (прибыли и налога с оборота). Межфирменные балансы могут разрабатываться на плановый и отчетный периоды в стоимостном, натуральном и натурально-стоимостном выражении, в зависимости от этого меняется форма и содержание отражения экономических процессов. В межфирменном балансе выделяют «чистые фирмы» - совокупность производств, выпускающих однородную продукцию.

При построении статической открытой модели межфирменного баланса принимают следующие допущения:

· производственную систему можно разбить на фирм (или продуктов);

· на каждой фирме производится только один продукт и одним способом, т.е. фиксируется технология получения продукта (это допущение не учитывается при решении задач оптимизации);

· вся продукция делится на промежуточную и конечную продукцию.

Промежуточной называют ту часть валовой продукции, которая идет в дальнейшую переработку на фирме и образует текущие материальные затраты. Конечной называют оставшуюся часть валовой продукции, которая окончательно уходит из производственного процесса годового производства и используется для потребления, накопления, экспорта.

Введем обозначения: ; - соответственно интенсивность валового и конечного продукта - ой фирмы; - интенсивность межфирменного потока продукции из - ой фирмы на воспроизводство единицы валовой продукции - ой фирмы.

Тогда распределение валовой продукции фирм примет вид:

(9)

Примем, что межфирменные поставки продукции - ой фирмы в - ю фирму линейно зависят от объема валовой продукции потребителя и нормы материалоемкости , определяющей затраты продукции - ой фирмы на воспроизводство единицы валовой продукции - ой фирмы. Тогда система (9) запишется в виде

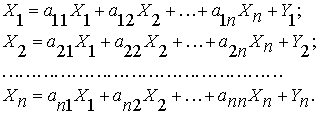(10)

Система (10) представляет собой математическую модель межфирменного баланса. Запишем ее в матричной форме

(11)

где 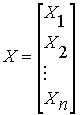; ; 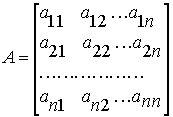- соответственно вектор интенсивности валового и конечного продукта; нормативная матрица материалоемкости (матрица коэффициентов прямых затрат).

Система линейных алгебраических уравнений (11) содержит 2 неизвестных (элементы векторов валового и конечного продуктов). Для получения решения фиксируют, например, элементы вектора валового продукта и по ним определяют элементы вектора конечного продукта () или по фиксированному вектору конечного продукта определяют вектор валового продукта (). В итоге имеем две задачи: наблюдаемости и синтеза.

Задача наблюдаемости () отражает процесс распределения валового продукта. Математическая модель задачи записывается в виде

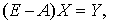(12)

где - единичная матрица.

Задача синтеза () отражает содержание процесса планирования валовой продукции по заданному вектору конечной продукции, т.е. ставится задача определить плановый объем валового продукта для обеспечения желаемого выпуска конечной продукции. Эта задача называется задачей планирования. Математическая модель задачи:

(13)

где символ «-1» является признаком обратной матрицы.

Модели (12) и (13) позволяют установить систему взаимосвязанных показателей, но они не могут определить эффективность того или иного плана.

По экономическому содержанию матрица материалоемкости неотрицательна, так как Неотрицательность решения определяется продуктивностью матрицы . Для обеспечения продуктивности неотрицательной матрицы должно выполняться одно из условий:

· максимальное собственное число матрицы меньше единицы <1;

· матрица неотрицательно обратима, т.е. существует обратная матрица и все ее элементы неотрицательны;

· последовательные главные миноры матрицы положительны.

Элементы матрицы представляют собой затраты валовой продукции - ой фирмы на воспроизводство единицы конечной продукции - ой фирмы. Их называют коэффициентами полных затрат. Матрица коэффициентов косвенных затрат равна разности матриц коэффициентов полных затрат и прямых затрат .

Пример 1 [2]. На плановый год заданы матрица коэффициентов прямых затрат и вектор конечного продукта:

Определить вектор валового продукта и межфирменные потоки

Для определения вектора валового продукта и межфирменных потоков используем математическую модель планирования и распределения продукции

Межфирменные потоки определяются соотношениями т.е. элементы первого столбца матрицы межфирменных потоков получаются умножением элементов первого столбца матрицы на первый элемент вектора , элементы второго столбца матрицы межфирменных - умножением элементов второго столбца матрицы на второй элемент вектора и т.д. Решение выполняем в среде электронных таблиц (ЭТ). Результаты расчета представлены в таблице 2, схема планового межфирменного баланса - в таблице 1.

Т а б л и ц а 1

Схема планового межфирменного баланса

Производящая фирма	Распределение по потребляющим фирмам			Конечный продукт	Валовой продукт
	1	2	3
1	69,526	4,232	4,596	153,4	231,754
2	18,54	11,286	0	17,2	47,026
3	16,222	2,822	0	38,4	57,444

Т а б л и ц а 2

Результаты расчета

В модели межфирменного баланса не выполняются расчеты затрат труда и основных производственных фондов на реализацию плана. Эти расчеты проводят после определения планируемого вектора валовой продукции в следующей последовательности.

На основе отчетных балансов получают нормы трудоемкости каждой фирмы где - норма трудоемкости - ой фирмы в отчетном году, - затраты труда - ой фирмы в отчетном году, - валовой продукт - ой фирмы в отчетном году. Нормы трудоемкости, полученные расчетным путем из отчетного баланса, корректируют для планового баланса. В итоге планируемый баланс труда принимает вид

(14)

где - норма трудоемкости - ой отрасли в планируемом году, - валовой продукт - ой отрасли в планируемом году. При прогнозировании трудовых ресурсов на планируемый период оценивают обеспеченность плана по труду путем сравнения планируемого баланса труда с прогнозируемым балансом. Если окажется, что , то планируемый вектор валового продукта не обеспечивается трудовыми ресурсами. Следовательно, нужно выбирать новый вариант с измененным вектором конечного продукта .

Аналогично выполняется расчет обеспеченности плана основными производственными фондами. Из отчетного баланса определяются нормы фондоемкости где - норма фондоемкости - ой фирмы в отчетном году, - основные производственные фонды - ой фирмы на конец отчетного периода, - валовой продукт - ой фирмы в отчетном году. На планируемый год эти нормы корректируют и составляют планируемый баланс основных производственных фондов:

. (15)

Планируемые основные производственные фонды сравниваются с прогнозируемыми фондами. В случае расчеты повторяются для нового варианта конечного продукта .

Если выпускаемая фирмами продукция не идет на развитие их производственной мощности, то уравнение мощности имеет вид

(16)

Тогда при постоянных фондоемкостях и коэффициентах выбытия ОПФ имеем

,

т.е. мощность – убывающая функция. Мощность убывает за счет выбытия, старения ОПФ. Автор работы [1] считает, что при переменной фондоемкости мощность может сохраняться или даже увеличиваться. Переменность фондоемкости означает, что на фирме имеются организационные, структурные изменения. При этом развитие фирмы происходит не в смысле простого роста мощности, а в смысле качественного изменения фирмы.

Дифференциальное уравнение мощности одной фирмы при переменном значении фондоемкости и вложении ОПФ в развитие производства имеет вид:

, (17)

где .

Дифференциальное уравнение фондоемкости [4]:

(18)

где - обобщенный технико-экономический показатель отражения уровня научно-технического развития фирмы, имеет решение

(19)

После подстановки (18) и (19) в уравнение (17) получим

(20)

Решение уравнения (2.20) имеет вид:

. (21)

Если не вкладывать ОПФ в развитие производства, т.е. , тогда

. (22)

На рис. 3 представлены результаты моделирования производственной мощности фирмы в зависимости от по формуле (22), на рис. 4 – по формуле (21).

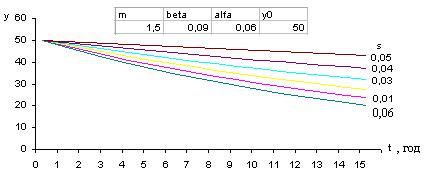
Рис. 3. Производственная мощность фирмы без вложения ОПФ в ее развитие

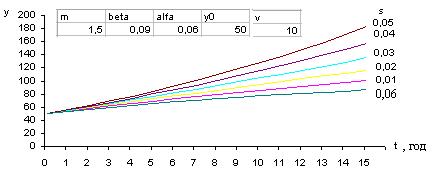
Рис. 4. Производственная мощность фирмы с вложением ОПФ в ее развитие

Анализ графиков показывает, что без вложения ОПФ в развитие производства фирма быстро прекращает свое существование (рис. 2.3). Для функционирования фирмы требуется хотя бы небольшое вложение ОПФ в развитие собственного производства (рис. 2.4).

Возможно, что поставки других фирм производственной системы, помогут фирме в наращивании мощности.

Литература:

1. Сиразетдинов Т.К. Динамическое моделирование экономических объектов. – Казань: «Фан», 1996. – 223 с.

2. Основы теории оптимального управления/Под ред. В.Ф. Кротова. – М.: Высшая школа, 1990. – 430 с.

3. Ершова Н.М. Методы и способы компьютерных информационных технологий: Конспект лекций. – Днепропетровск: ПГАСА, 2005. – 169 с.

4. Крушев В.Н. Теория управления. Технико-экономические системы: Учебное пособие. – Казань: Изд-во Казан. гос. техн. ун-та, 2004. – 134 с.