Candidate of technical sciences Р. V. Tereliansky

Volgograd state technical university, Russia

PROGRAM REALIZATION OF THE ANALYSIS OF EXPERT ESTIMATIONS IN THE ASSIGNED CONFIDENCE INTERVALS

It is proposed to carry out paired comparisons during the organization of examinations with the use of the parametrically assigned functions in the book [1]. Each function corresponds to the conventional idea of trends – linear, it is exponential or to logarithmically increasing (diminishing), oscillating, quadratic, etc. Practice shows that frequently the experts can not give precise value for the paired comparison of the elements of system for some specific moment in the future. For example, they can not assert with the hundred percent confidence that “in the month of alternative A will have very strong superiority of preference over the alternative B on the criterion C” (number 9 in the scale [1]). The task of a certain interval of preferences for each moment of time t would be more logical, i.e., preference can accept value from “strong superiority” (number 5) to “significant superiority” (number 7) at the given moment. With a similar approach we obtain two curves f₁ and f₂, which limit the range of change in the preferences in the time interval, for which the forecast is created (Fig. 1).

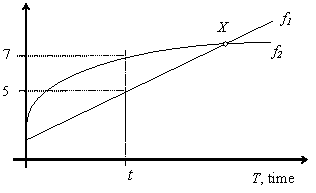
Fig. 1. Interval Description of Expert’s Estimations

on the Plane of the Preferences

How must be produced calculations in this case? Here is the following algorithm:

1. We obtain two value of preference for each point of X-axis according to the assigned functions (f₁ and f₂ on fig. 1), i.e., two matrices of paired comparisons automatically are formed for each moment of time.

2. The vectors of local priorities on the basis of the analysis of two matrices are calculated.

3. The convolution is produced for the entire system of estimations, and two vectors of the global priorities are calculated.

4. Each vector remains in the appropriate table with the indication of moment of time, for which the calculation is produced.

5. Steps 1- 4 are repeated for entire forecasted interval.

6. The obtained tables are processed by any of the known interpolation methods for obtaining the resulting curves.

The result of the work of the this algorithm will be two curves, which limit the possible range of change in the preference of alternatives relative to purpose a study (focus of hierarchy). It is possible to recommend the integral estimation I_e for the evaluation of the accuracy of the obtained forecast:

,

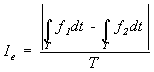where Т – the time interval, for which is comprised the forecast, f₁ and f₂ – the functions, assigned by the expert. In this case the outer limits of accuracy for the scale will be the numbers close to 9 and 0. We will obtain the number approximately equal to 9, if expert indicates entire range of the scale (number from 1/9 to 9) as the possible interval, but that is completely inadmissible. We will obtain the number equal to zero, in the completely opposite case, i.e., if both functions in the forecasted interval coincided (for example as at point X in Fig. 1). It should be noted, that the application of the scale of designations requires additional analysis and transformation of matrices. It is explained, that it was sufficiently difficult to work with the parametrically represented functions for experts, whose activity was not connected with the algebraic idea of knowledge (for example, sociologists, supply workers, administrators, etc). However, basic deficiency consists in the attempt to tie function to the boundaries of the scale 1/9 - 9. The fact is that the distribution of the elements of the scale on the coordinate axis is extremely uneven. There is in the form “a plane of preferences”: along the Y-axis - the numerical estimation of preference, while along the X-axis – time (Fig. 1). In this case, the semantically intelligible expression of the expert: “The preference of alternative A above the alternative B evenly grows from the estimation “very strong superiority B over A” (1/9) to “very strong superiority A over B” (9), must occur, by straight line (function – a1*(t+a2)), and on the plane of preferences it appears faster as the branch of hyperbola. A similar nonconformity of the semantic and parametric representation of function frequently starts expert, who composes the forecast of the dynamics of preferences, into the blind alley, which, as a result, leads to obtaining of inaccurate or completely improbable result. Output from the created position could be the evenness distribution of the elements compulsorily of integral estimations on the axis of preferences. For example, in the book [1] a similar scale was used for determining the variable states with the description of the process of analytical planning. Interpreting this scale for the tasks of decision making, its numerical idea can be described thus:

1. Zero – the alternatives do not have preferences above each other, i.e., this is “equal importance”.

2. “2 “ – “weak superiority” one alternative over another.

3. “ 4 ” – “Moderate superiority”.

4. “ 6 “ – “Strong superiority”.

5. “ 8 “ – “Significant superiority”.

6. Numbers 1,3,5,7 are used as intermediate between two adjacent.

7. Negative integers -1… - 8 are used for the reverse estimations with the filling of the matrix of paired comparisons.

The application of positive and negative estimations and zero is semantically understandable. If alternative is worse - estimation is negative, if it is better - it is positive, the absence of preferences is natural to designate by zero. On “the planes of preferences” in this case “linear increase in the preferences” will appear precisely as a linear increase in the graph. Furthermore, as a result the analysis of the opinions of experts, which worked with the data by the method, it was explained by them that it is not entirely convenient to use mathematical functions for describing the dynamics of preferences, it is much more convenient and more reliable it would be indicate what, in their opinion, preferences will have the alternative at a certain specific moment of time. The expert does not desire to be conveyed with the selection of the parameters for the function and with the selection of function itself, in this case. Computer system must allow expert to place the priorities in the form of points on the plane of preferences, and the function of preferences program must select itself, in this case. Using contemporary computational power, computer program can conduct interpolation in the interactive regime, freeing expert from the need for defining concretely the inaccurate and incomplete knowledge available to it. Carried into matrix points of paired comparisons dynamic preferences, can be processed, designing the values of the functions of preferences for each moment of time [2] indicated. Obtained thus matrix of paired comparisons loses a number of the valuable properties, inherent to positive in square matrices. For example, it is sufficiently difficult to use the algorithms of the calculation of the eigenvalue of matrix, indices of coordination and relation of the coordinations (with this calculation procedure it is great the probability of appearance in the vector of the priorities of imaginary unit). To avoid similar difficulties is possible, if we will add to the module of each number in the matrix 1, before the calculations of the eigenvector, and multiply on -1 the numbers are smaller than zero and elevate into -1 degrees, and conduct further calculations. Obtained thus vectors of the priorities (their quantity will be equal to a quantity of moments of time, for which it is comprised forecast) can be processed by any known approximation method for obtaining the functional, and then graphic idea of a change in the dynamics of preferences. The program system, which makes it possible to introduce the description of the system of the preferences in the form of hierarchy being investigated, to introduce and to edit the set of the matrices of the paired comparisons, elements of which they will be the functional idea of the dynamics of priorities is created. The eigenvectors of the positive matrices of paired comparisons are calculated with the use of an iterative (through the limit of the relation of the works of MPC to the unit vectors and the column vectors) or approximate (through the geometric mean) algorithm. The approximate algorithm of calculation gives the result with accuracy to of the order of the ranking of elements and is used for the large hierarchies and the prolonged forecast intervals. The analysis of the set of the obtained vectors of priorities is produced with the aid of the method of least squares. The results of analysis are represented in the form of graphs and table, which contains the parametric representation of the selected dependences of priorities on the time. Program product is written with the use of a system of programming Borland C++ 4.5 with the use of a library OWL 2.0 for Windows.

Literature:

1. Саати, Т. Принятие решений. Метод анализа иерархий : [пер. с англ.] / Т. Саати. – М.: Радио и связь. 1993. – 316с.

2. Терелянский, П.В. Информационные технологии прогнозирования технических решений на основе нечетких и иерархических моделей : монография / П.В. Терелянский, А.В. Андрейчиков. – Волгоград : ВолгГТУ, 2007. – 204 с.