Физика/6.
Радиофизика
Калиберда М.Е., Погарский С.А.
Харьковский национальный университет им. В.Н. Каразина, Украина
Дифракция волн на системе лент в плоском волноводе
Задачи
дифракции волн на различных системах волноводных неоднородностей представляют несомненный
интерес для радиофизики. Можно найти ряд работ, в которых решались подобного
рода задачи. К примеру, в работе [1] рассматривается волновод с резонансными
вставками в виде периодической гребенки. Для исследования неоднородностей в
волноводе в [2] использован метод, основывающийся на расширенном принципе
Гюйгенса и методе конечных элементов для интегральных уравнений. В [3]
рассматривается волновод, периодически заполненный слоями диэлектрика.
В
данной работе операторный метод [4] применяется для решения задачи дифракции
собственных волн плоского волновода на системе лент.
Ключевая задача для одной ленты
Будем
рассматривать структуру, представленную на рис.1. Стенки волновода и лены
бесконечно проводящие. Волновод заполнен неидеальным диэлектриком с
диэлектрической проницаемостью ![]() . Основная идея использования операторного метода состоит в
решении “ключевой задачи” – задачи дифракции на одной ленте.
. Основная идея использования операторного метода состоит в
решении “ключевой задачи” – задачи дифракции на одной ленте.
 В случае
В случае ![]() - волн представим единственную отличную от нуля компоненту
магнитного поля в виде
- волн представим единственную отличную от нуля компоненту
магнитного поля в виде
 ,
,
где
![]()
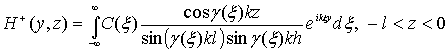 ,
,
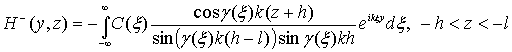 , (1)
, (1)
Неизвестная спектральная функция ![]() может быть определена из парного
интегрального уравнения:
может быть определена из парного
интегрального уравнения:
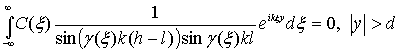 , (2)
, (2)
 . (3)
. (3)
Из уравнения (2) следует, что функция ![]() может быть разложена в ряд [5]
может быть разложена в ряд [5]
![]() ,
,
где 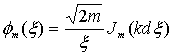 ,
, ![]() ,
, ![]() – функции Бесселя.
Таким образом, после преобразований уравнения (3) получаем две независимые
системы линейных алгебраических уравнений для определения коэффициентов
– функции Бесселя.
Таким образом, после преобразований уравнения (3) получаем две независимые
системы линейных алгебраических уравнений для определения коэффициентов ![]()
![]() ,
,
где
![]()
![]() ,
,
 .
.
Численные результаты
 Используя представленный алгоритм,
проведен цикл математического моделирования значений коэффициентов прохождения
и отражения. На рис.2 представлены зависимости коэффициента прохождения от
длины ленты для различных значений параметра
Используя представленный алгоритм,
проведен цикл математического моделирования значений коэффициентов прохождения
и отражения. На рис.2 представлены зависимости коэффициента прохождения от
длины ленты для различных значений параметра ![]() (
(![]() – сплошная линия,
– сплошная линия, ![]() – пунктирная линия,
– пунктирная линия, ![]() – линия из точек). Как видно из рисунка,
существуют такие значения параметров, при которых коэффициент прохождения равен
приблизительно нулю или единице. Таким образом, структура может работать в
запирающем или пропускающем режиме.
– линия из точек). Как видно из рисунка,
существуют такие значения параметров, при которых коэффициент прохождения равен
приблизительно нулю или единице. Таким образом, структура может работать в
запирающем или пропускающем режиме.
 Зависимости
коэффициента отражения от расстояния между лентами для структуры, состоящей из
четырех и десяти лент, представлены на рис.3. Рисунки отражают типичные
зависимости полосы запирания от числа неоднородностей, а именно ее сужение при
увеличении числа неоднородностей и наличие определенного числа осцилляций в
полосе пропускания (число локальных минимумов на единицу меньше числа
неоднородностей).
Зависимости
коэффициента отражения от расстояния между лентами для структуры, состоящей из
четырех и десяти лент, представлены на рис.3. Рисунки отражают типичные
зависимости полосы запирания от числа неоднородностей, а именно ее сужение при
увеличении числа неоднородностей и наличие определенного числа осцилляций в
полосе пропускания (число локальных минимумов на единицу меньше числа
неоднородностей).
Заключение
Представленный
алгоритм, который был применен к решению задачи дифракции собственных волн
плоского волновода на системе лент достаточно универсальный. Это объясняется
определенным формализмом процедуры определения операторов отражения и
прохождения структуры с конечным числом препятствий, если известны
соответствующие операторы отражения и прохождения одиночного препятствия.
Предложенная модель может быть использована для создания частотно-селективных
устройств.
Литература:
1.
George Goussetis, Alexandros P. Feresidis, Panagiotis Kosmas. Efficient
analysis, design, and filter applications of EBG waveguide with periodic
resonant loads// IEEE transactions on microwave theory and techniques. - 2006.
- Vol. 54. - № 11. - P. 3885-3892.
2.
Riana H. Geschke, Ronald L. Ferrari, David Bruce Davison, Petrie meyer.
The solution of weveguide scattering problems by application of an extended
Huygens formulation// IEEE transactions on microwave theory and techniques. –
2006. – Vol. 54. – № 10. – P. 3698-3705.
3.
Hui Kan Liu, Tian Lin Dong. Propagation characteristics for periodic
waveguide based on generalized conservation of complex power technique// IEEE
transactions on microwave theory and techniques. – 2006. – Vol. 54. – № 9. – P.
3479–3485.
4.
Литвиненко Л.М., Рєзник І.І., Литвиненко Д.Л. Дифракція хвиль на
напівнескінченних періодичних структурах // Доповіді АН Української РСР. -
1991. - №6. - С. 62-66.
5. Литвиненко
Л.Н., Просвирнин С.Л. Поперечная щель в плоском волноводе// Радиотехника и электроника. –
1977. – Т.
22, № 7. – С.1321-1326.