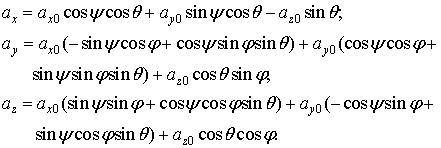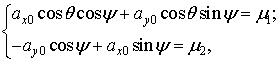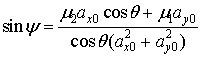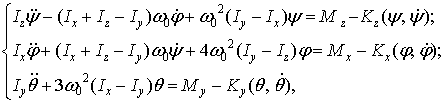Рыжков Л.М., Степуренко Д.И., Шилко И.С.

Национальный технический университет Украины «КПИ»

УПРАВЛЕНИЕ МИКРОСПУТНИКОМ ПРИ НЕПОЛНОЙ ИНФОРМАЦИИ ОБ ЕГО ПРОСТРАНСТВЕННОМ ПОЛОЖЕНИИ

Одной из проблем при управлении микроспутником (МС) является отсутствие полной информации об его пространственном положении. Это объясняется тем, что все измерители углового положения МС являются одновекторными. В то же время для определения пространственного положения МС необходима информация о двух векторах. Такой подход используется в алгоритме TRIAD [1,2], где измеряются проекции двух векторов на оси связанной и орбитальной систем координат. Далее матричным методом вычисляются направляющие косинусы между этими системами координат.

Будем считать известными углы тангажа и крена (измеряются датчиком Земли), а также три проекции вектора индукции магнитного поля Земли на оси связанной системы координат (измеряются магнитометрами) и орбитальной системы координат (вычисляются в вычислителе). Рассмотрим управление МС при отсутствии измерителя угла рыскания. Задача заключается в том, чтобы на основе имеющейся информации вычислить угол рыскания и использовать его для управления.

Движение МС будем рассматривать в орбитальной системе координат (рис.1), где - орбитальная угловая скорость. Взаимное положение орбитальной системы координат и системы координат, связанной с МС, показано на рис.2.

Используя рис.2, получим следующие соотношения:

(1)

Для нахождения угла рыскания поступим следующим образом. Преобразуем второе и третье уравнение системы (1):

(2)

где .

Из системы (2) получим следующее выражение для вычисления угла :

(3)

На основе выражения (3) строится вычислитель угла . Для этого необходимо знать проекции вектора индукции магнитного поля Земли на оси орбитальной (вычисляются) и связанной (измеряются магнитометрами) систем координат. Углы и измеряются датчиком Земли.

Заметим, что для полярной орбиты при значениях аргумента широты 90⁰ и 270⁰ алгоритм не функционирует. Это объясняется тем, в этих точках орбиты вектор магнитного поля Земли и местная вертикаль совпадают, то есть двухвекторная система оценивания превращается в одновекторную. Отметим, что в этом случае не функционирует и алгоритм TRIAD.

Для оценки эффективности управления движением спутника при использовании предложенного вычислителя проведем моделирование движения МС.

Уравнение движения запишем в форме:

(4)

где - осевые моменты инерции МС; ,,- коэффициенты передачи регуляторов; М_х, М_у, М_z - возмущающие моменты.

При моделировании приняты следующие исходные данные: кг·м², кг·м², кг·м², =0,0012 с^-1, Н·м, Н·м, Н·м. Начальное значение каждого угла равняется 0,1 рад.

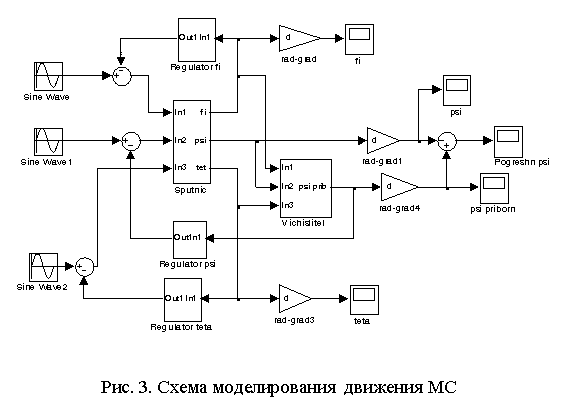
Схема моделирования движения МС в среде MATLAB показана на рис. 3, где в блоке «Sputnic» реализованы уравнения (4). В блоке «Vichislitel», выходом которого является вычисленное значение угла , реализована формула (3). В блоках «Regulator fi», «Regulator psi», «Regulator teta» реализованы регуляторы системы управления движением МС. Передаточные функции регуляторов приняты в виде:

В блоках «Sine Wave», «Sine Wave1», «Sine Wave2» задаются возмущающие моменты.

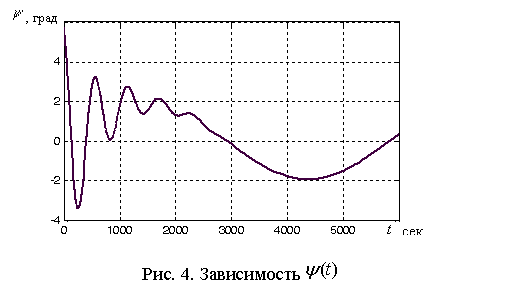
На рис. 4 приведена зависимость от времени угла , которая характеризует как переходный, так и установившийся процесс.

Видим, что приблизительно через 3000 секунд устанавливаются колебания с амплитудой около 2⁰, что является приемлемым с учетом требований к точности системы управления МС.

Таким образом, предложенный алгоритм вычисления угла рыскания позволяет построить эффективную систему управления движением МС и обеспечить надлежащую точность ориентации.

Список литературы

1. Shuster M.D., Oh S.D. Three-Axes Attitude Determination from Vector Observation // Journal of Guidance and Control. – 1981. - Vol. 4 №1 – P.70-77.

2. Krogh K., Shreder E. Attitude determination for AAU CuberSat // Aalborg University: Department of Control Engineering. - 2002. – P. 133.

3. Коваленко А.П. Магнитные системы управления космическими летательными аппаратами. – М.: Машиностроение, 1975.– 247 с.